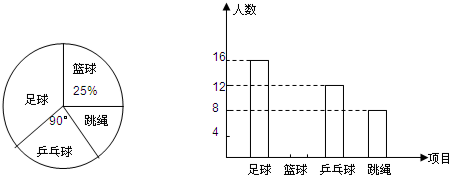
题目内容
14. 如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.
如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.
分析 分两种情况考虑:B′在横对称轴上与B′在竖对称轴上,分别求出BF的长即可.
解答 解:当B′在横对称轴上,此时AE=EB=3,如图1所示,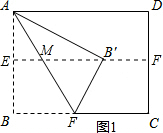
由折叠可得△ABF≌△AB′F,
∴∠AFB=∠AFB′,AB=AB′=6,BF=B′F,
∴∠B′MF=∠B′FM,
∴B′M=B′F,
∵EB′∥BF,且E为AB中点,
∴M为AF中点,即EM为中位线,∠B′MF=∠MFB,
∴EM=$\frac{1}{2}$BF,
设BF=x,则有B′M=B′F=BF=x,EM=$\frac{1}{2}$x,即EB′=$\frac{3}{2}$x,
在Rt△AEB′中,根据勾股定理得:32+($\frac{3}{2}$x)2=62,
解得:x=2$\sqrt{3}$,即BF=2$\sqrt{3}$;
当B′在竖对称轴上时,此时AM=MD=BN=CN=4,如图2所示: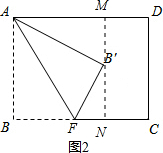
设BF=x,B′N=y,则有FN=4-x,
在Rt△FNB′中,根据勾股定理得:y2+(4-x)2=x2,
∵∠AB′F=90°,
∴∠AB′M+∠NB′F=90°,
∵∠B′FN+∠NB′F=90°,
∴∠B′FN=∠AB′M,
∵∠AMB′=∠B′NF=90°,
∴△AMB′∽△B′NF,
∴$\frac{AM}{B′N}$=$\frac{AB′}{B′F}$,即$\frac{4}{y}$=$\frac{6}{x}$,
∴y=$\frac{2}{3}$x,
∴($\frac{2}{3}$x)2+(4-x)2=x2,
解得x1=9+3$\sqrt{5}$,x2=9-3$\sqrt{5}$,
∵9+3$\sqrt{5}$>4,舍去,
∴x=9-3$\sqrt{5}$
所以BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$,
故答案为$2\sqrt{3}$或$9-3\sqrt{5}$.
点评 本题考查了折叠的性质,三角形中位线的性质,三角形相似的判定和性质以及勾股定理的应用,注意分两种情况解答此题.

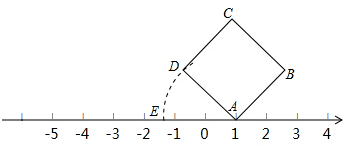 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )| A. | $-\sqrt{5}$ | B. | $1-\sqrt{5}$ | C. | $\frac{{-1-\sqrt{5}}}{2}$ | D. | $\frac{3}{2}-\sqrt{5}$ |
| A. | x=$\frac{a+b}{2}$ | B. | x=$\sqrt{ab}$ | C. | a2-b2=x2 | D. | $\frac{1}{x}$=$\frac{1}{a}$+$\frac{1}{b}$ |
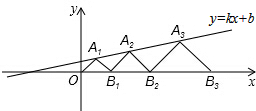 如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).
如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).