题目内容
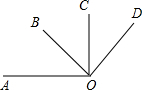
11.如图,O为直线AB上一点,∠BOC=α.(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=$\frac{1}{3}$∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
(3)若∠AOD=$\frac{1}{n}$∠AOC,∠DOE=$\frac{180°}{n}$(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).

分析 (1)利用角平分线的性质得出∠AOD=∠DOC=70°,进而得出∠AOE的度数;
(2)利用设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,得出x的值,进而用α表示∠AOE的度数;
(3)利用(2)中作法,得出x与α的关系,进而得出答案.
解答 解:(1)∵∠BOC=40°,OD平分∠AOC,
∴∠AOD=∠DOC=70°,
∵∠DOE=90°,则∠AOE=90°-70°=20°;
故答案为:20°;
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,
解得:x=$\frac{180-α}{3}$,
∴∠AOE=60-x=60-$\frac{180-α}{3}$=$\frac{1}{3}$α;
(3)设∠AOD=x,则∠DOC=(n-1)x,∠BOC=180-nx=α,
解得:x=$\frac{180-α}{n}$,
∴∠AOE=$\frac{180}{n}$$\frac{180-α}{n}$=$\frac{α}{n}$.
点评 此题主要考查了角的计算,正确根据角之间的数量关系得出等式是解题关键.

练习册系列答案
相关题目
3.下列各式的计算中,正确的是( )
| A. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$=6 | B. | ($\sqrt{3}$-1)2=3-1=2 | ||
| C. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{81}$×$\sqrt{1}$=9 | D. | 3$\sqrt{\frac{2}{3}}$=$\sqrt{2}$ |
19.如果A和B是一个直角三角形的两个锐角,那么( )
| A. | sinA=cosB | B. | sinA=sinB | C. | cosA=cosB | D. | sinB=cosB |
20.嫦娥三号于2015年12月14日晚21时11分11秒成功落月,着陆地点为虹湾,这是月球上最突丽的地标之一,它其实是一个直径达 260000m 的巨型陨石坑壁.虹湾的直径用科学记数法表示为( )m.
| A. | 2.6×105 | B. | 26×104 | C. | 2.6×104 | D. | 0.26×106 |
 如图,若∠AOD=120°,∠BOC=70°,且∠AOC:∠BOD=9:10,则∠AOB=20°.
如图,若∠AOD=120°,∠BOC=70°,且∠AOC:∠BOD=9:10,则∠AOB=20°. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为2.
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为2.