题目内容
16.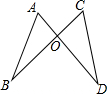 如图,线段AD、BC相交于点O,连接AB、CD.下列条件:①AB=CD,AO=CO;②∠A=∠C,AO=CO;③AO=CO,BO=DO;④∠B=∠D,AB=CD;⑤∠B=∠D,∠A=∠C;从中任选一组能得出△ABO≌△CDO的概率是$\frac{3}{5}$.
如图,线段AD、BC相交于点O,连接AB、CD.下列条件:①AB=CD,AO=CO;②∠A=∠C,AO=CO;③AO=CO,BO=DO;④∠B=∠D,AB=CD;⑤∠B=∠D,∠A=∠C;从中任选一组能得出△ABO≌△CDO的概率是$\frac{3}{5}$.
分析 根据三角形全等的判定逐一判断,再根据概率可得答案.
解答 解:在△ABO和△CDO中,
②∵$\left\{\begin{array}{l}{∠A=∠C}\\{AO=CO}\\{∠AOB=∠COD}\end{array}\right.$,
∴△ABO≌△CDO(ASA);
③∵$\left\{\begin{array}{l}{AO=CO}\\{∠AOB=∠COD}\\{BO=DO}\end{array}\right.$,
∴△ABO≌△CDO(SAS),
④∵$\left\{\begin{array}{l}{∠B=∠D}\\{∠AOB=∠COD}\\{AB=CD}\end{array}\right.$,
∴△ABO≌△CDO(AAS),
则在以上所列5个条件中,能使两三角形全等的条件有②③④这3个,
∴从中任选一组能得出△ABO≌△CDO的概率是$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题主要考查全等三角形的判定与概率公式,熟练掌握全等三角形的判定是解题的关键.

练习册系列答案
相关题目
13.下列实数中,是无理数的是( )
| A. | $\frac{22}{7}$ | B. | 3.14 | C. | 6.$\stackrel{••}{66}$ | D. | $\frac{\sqrt{2}}{2}$ |
4.下列选项中不属于平行四边形的性质的是( )
| A. | 一组对角相等 | B. | 对角线互相平分 | ||
| C. | 一组对边平行相等 | D. | 对角线互相垂直 |
1.要使分式$\frac{{a}^{2}-9}{a+3}$的值为零,则a的值为( )
| A. | a=0 | B. | a=3 | C. | a=-3 | D. | a=±3 |
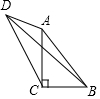 在Rt△ABC中,∠ACB=90°,点D为△ABC外一点,连接AD、CD、∠ADC=45°,连接BD,∠DBC=2∠ADB,AB=5,BD=7,则BC=3或4.
在Rt△ABC中,∠ACB=90°,点D为△ABC外一点,连接AD、CD、∠ADC=45°,连接BD,∠DBC=2∠ADB,AB=5,BD=7,则BC=3或4.