题目内容
19.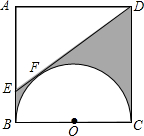 如图,以正方形ABCD边BC为直径作半圆O,过点D作直线与半圆相切于点F,交AB于点E,若AB=2cm.求:
如图,以正方形ABCD边BC为直径作半圆O,过点D作直线与半圆相切于点F,交AB于点E,若AB=2cm.求:(1)AE的长;
(2)阴影部分的面积.
分析 (1)由切线长定理可知:BE=EF、DF=DC=2,设AE=xcm,则EF=(2-x)cm,故此ED=(4-x)cm,然后在Rt△ADE中依据勾股定理列方程求解即可;
(2)阴影部分的面积=正方形的面积-△ADE的面积-减去半圆的面积.
解答 解:(1)切线长定理可知:BE=EF、DF=DC=2cm.
设AE=xcm,则EF=(2-x)cm,ED=(4-x)cm.
在Rt△ADE中,AD2+AE2=ED2,即22+x2=(4-x)2.
解得:x=1.5.
则AE=1.5cm.
(2)阴影部分的面积=正方形的面积-△ADE的面积-减去半圆的面积
=2×2-$\frac{1}{2}×\frac{3}{2}×2$-$\frac{1}{2}×π×{1}^{2}$
=$\frac{5-π}{2}$cm2.
阴影部分的面积为$\frac{5-π}{2}$cm2.
点评 本题主要考查的是切线的性质、切线长定理、勾股定理,依据切线长定理、勾股定理列出关于x的方程是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
7.把连续奇数列成下表:
(1)表中的m值是19:
(2)第6行、第5列的数字是65;
(3)请用一个长方形方框框住表中的四个数字,交叉相乘,再将乘积相减.看看你能发现什么结论,用文字语言表述你的结论.并用整式运算证明你的结论.
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | 第六列 | 第七列 | |
| 第1行 | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 第2行 | 15 | 17 | m | 21 | 23 | 25 | 27 |
| 第3行 | 29 | 31 | 33 | 35 | 37 | 39 | 41 |
| 第4行 | 43 | 45 | 47 | 49 | 51 | 53 | 55 |
| … |
(2)第6行、第5列的数字是65;
(3)请用一个长方形方框框住表中的四个数字,交叉相乘,再将乘积相减.看看你能发现什么结论,用文字语言表述你的结论.并用整式运算证明你的结论.
5.关于矩形性质,下列说法不正确的是( )
| A. | 四个角都是直角 | |
| B. | 既是轴对称图形,也是中心对称图形 | |
| C. | 对角线互相垂直 | |
| D. | 对角线互相平分且相等 |
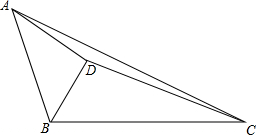 如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.
如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.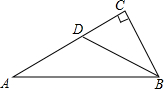 如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.
如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.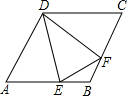 如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.
如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF. 直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)
直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)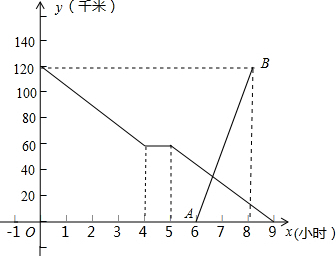 张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示.
张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示.