题目内容
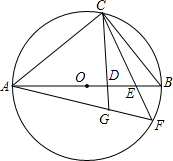 如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,
如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,(1)求证:△ACG∽△AFC;
(2)若AC=2
| 2 |
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)如图,作辅助线;首先证明∠F=∠ACG,结合∠CAG=∠FAC,即可解决问题.
(2)由△ACG∽△AFC,得到
=
,即可解决问题.
(2)由△ACG∽△AFC,得到
| AC |
| AF |
| AG |
| AC |
解答: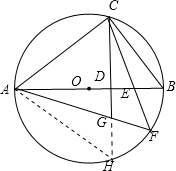 解:(1)如图,
解:(1)如图,
延长CG,交⊙O于点H;连接AH;
∵CD⊥AB,
∴
=
,
∴∠F=∠ACG,而∠CAG=∠FAC,
∴△ACG∽△AFC.
(2)∵△ACG∽△AFC,
∴
=
,
∴AC2=AF•AG,而AC=2
,
∴AF•AG=8.
 解:(1)如图,
解:(1)如图,延长CG,交⊙O于点H;连接AH;
∵CD⊥AB,
∴
 |
| AC |
 |
| AH |
∴∠F=∠ACG,而∠CAG=∠FAC,
∴△ACG∽△AFC.
(2)∵△ACG∽△AFC,
∴
| AC |
| AF |
| AG |
| AC |
∴AC2=AF•AG,而AC=2
| 2 |
∴AF•AG=8.
点评:该题主要考查了圆周角定理、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线,灵活运用圆周角定理、相似三角形的判定及其性质来分析、判断、解答.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
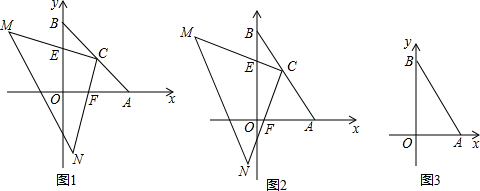
 如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC)
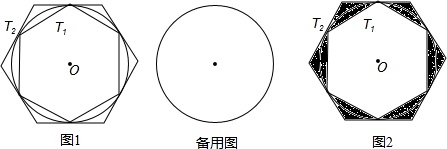
如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC) 如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )
如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )



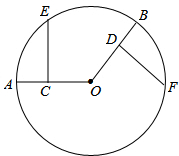 如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证:
如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证: