题目内容
如图1,T1,T2分别为⊙O的内接正六边形和外切正六边形.
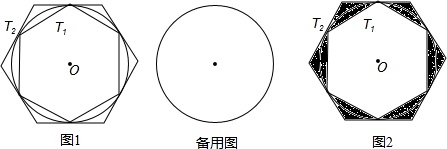
(1)请你在备用图中画出圆O的内接正六边形,并简要写出作法;
(2)设圆O的半径为R,求T2的面积(用含R的式子表示);
(3)设⊙O的半径为R,求图2中阴影部分的面积(用含R的式子表示).

(1)请你在备用图中画出圆O的内接正六边形,并简要写出作法;
(2)设圆O的半径为R,求T2的面积(用含R的式子表示);
(3)设⊙O的半径为R,求图2中阴影部分的面积(用含R的式子表示).
考点:正多边形和圆,扇形面积的计算
专题:
分析:(1)先画出60°的圆心角,确定圆心角所对的弧,在圆上依次截取与弧AB相等的弧即可;
(2)连接OG,得到Rt△OGB≌Rt△OGA,然后利用勾股定理解答;
(3)根据“阴影部分的面积=外切正六边形的面积-内接正六边形的面积”,并把正六边形的面积转化为六个三角形面积的和解答.
(2)连接OG,得到Rt△OGB≌Rt△OGA,然后利用勾股定理解答;
(3)根据“阴影部分的面积=外切正六边形的面积-内接正六边形的面积”,并把正六边形的面积转化为六个三角形面积的和解答.
解答:解:(1)如图
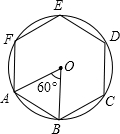
作法:①在⊙O中做圆心角∠AOB=60°;
②在⊙O上依次截取与弧AB相等的弧,得到圆的6个等分点A、B、C、D、E、F;
③顺次连接各点,六边形ABCDEF即为所求正六边形.
(2)如图:
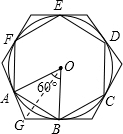
∵由(1)知△AOB为等边三角形,
∴T1的半径为R,
连接OG,可知Rt△OGB≌Rt△OGA,
∴∠OGB=60°,
∴BG=
,
设BG为x,由勾股定理有:x2+R2=(2x)2,
解得:x=
R,
外切正六边形的边长为
R.
(3)由图知:
阴影部分的面积=外切正六边形的面积-内接正六边形的面积,
∵内接正六边形的面积为S△AOB的六倍,S△AOB=
R2,
∴内接正六边形的面积为:S内=6S△AOB=
R2.
∵外切正六边形的面积为S△OGH的六倍,S△OGH=
R2,
∴外切正六边形的面积为:S外=6S△OGH=2
R2,
∴S阴=S外-S内=
R2.

作法:①在⊙O中做圆心角∠AOB=60°;
②在⊙O上依次截取与弧AB相等的弧,得到圆的6个等分点A、B、C、D、E、F;
③顺次连接各点,六边形ABCDEF即为所求正六边形.
(2)如图:

∵由(1)知△AOB为等边三角形,
∴T1的半径为R,
连接OG,可知Rt△OGB≌Rt△OGA,
∴∠OGB=60°,
∴BG=
| 1 |
| 2 |
设BG为x,由勾股定理有:x2+R2=(2x)2,
解得:x=
| ||
| 3 |
外切正六边形的边长为
2
| ||
| 3 |
(3)由图知:
阴影部分的面积=外切正六边形的面积-内接正六边形的面积,
∵内接正六边形的面积为S△AOB的六倍,S△AOB=
| ||
| 4 |
∴内接正六边形的面积为:S内=6S△AOB=
3
| ||
| 2 |
∵外切正六边形的面积为S△OGH的六倍,S△OGH=
| ||
| 3 |
∴外切正六边形的面积为:S外=6S△OGH=2
| 3 |
∴S阴=S外-S内=
| ||
| 2 |
点评:本题考查了正多边形和圆的有关知识,在计算正多边形中的有关量的时候,可以构造到由正多边形的半径、边心距、半边组成的直角三角形中,根据锐角三角函数进行计算.注意:相似多边形的面积比即是其相似比的平方.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
下列计算正确的是( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
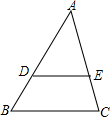 如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,AB=6,则DE:BC的值为( )
如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,AB=6,则DE:BC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
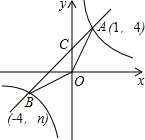 如图,已知:反比例函数y=
如图,已知:反比例函数y=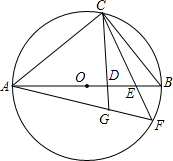 如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,
如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,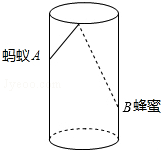 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为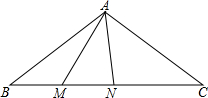 如图,ABC中,AB=AC,BC=16,cosB=
如图,ABC中,AB=AC,BC=16,cosB= 如图,在Rt△ABC中,∠C=90°,AC=6,tanA=
如图,在Rt△ABC中,∠C=90°,AC=6,tanA=