题目内容
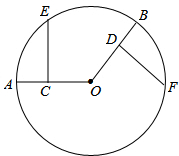 如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证:
如图,已知AO、BO分别是⊙O的两条半径,C、D分别是AO、BO的中点,CE⊥AO,DF⊥BO.求证: |
| AE |
 |
| BF |
考点:圆心角、弧、弦的关系
专题:证明题
分析:连结OE、OF,如图,由C、D分别是AO、BO的中点得到OC=OD,再根据HL证明Rt△OEC≌Rt△OFD,得到∠COE=∠DOF,然后根据圆心角、弧、弦的关系即可得到
=
.
 |
| AE |
 |
| BF |
解答: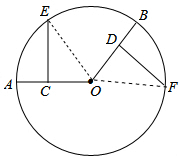 解:连结OE、OF,如图,
解:连结OE、OF,如图,
∵C、D分别是AO、BO的中点,
∴OC=OD,
∵CE⊥AO,DF⊥BO,
∴∠OCE=90°,∠ODF=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴
=
.
 解:连结OE、OF,如图,
解:连结OE、OF,如图,∵C、D分别是AO、BO的中点,
∴OC=OD,
∵CE⊥AO,DF⊥BO,
∴∠OCE=90°,∠ODF=90°,
在Rt△OEC和Rt△OFD中,
|
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴
 |
| AE |
 |
| BF |
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
当a<0时,|a-
|=( )
| 4a2 |
| A、a | B、-a | C、3a | D、-3a |
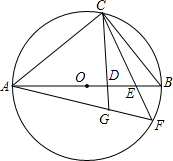 如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,
如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G, 如图,OC⊥AB,∠AOE=∠COF,则OE、OF是什么位置关系?请说明理由.
如图,OC⊥AB,∠AOE=∠COF,则OE、OF是什么位置关系?请说明理由.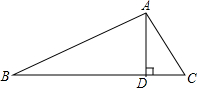 已知AB⊥AC于A,AD⊥BC于D,AB=8cm,AC=6cm,AD=4.8cm,BC=6.4cm,CD=3.6cm.
已知AB⊥AC于A,AD⊥BC于D,AB=8cm,AC=6cm,AD=4.8cm,BC=6.4cm,CD=3.6cm.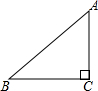 如图,在Rt△ABC中,∠C=90°,AC=6,tanA=
如图,在Rt△ABC中,∠C=90°,AC=6,tanA=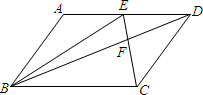 如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为
如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为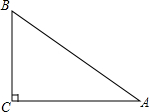 如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用?
如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用? 如图,已知∠A+∠DBA=180°,∠3=58°,求∠4的度数.
如图,已知∠A+∠DBA=180°,∠3=58°,求∠4的度数.