题目内容
 如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC)
如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC)考点:矩形的性质
专题:
分析:根据矩形的性质得出∠DCB=90°,AC=BD,AC=2CO,BD=2OD,求出OC=OD,得出△COD是等边三角形,求出∠ACB=30°,求出OC=CE,即可求出答案.
解答:解:∵∠AOB=60°,
∴∠DOC=∠AOB=60°,
∵四边形ABCD是矩形,
∴∠DCB=90°,AC=BD,AC=2CO,BD=2OD,
∴OC=OD,
∴△COD是等边三角形,
∴DC=OC,∠ACD=60°,
∴∠ACB=90°-60°=30°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠DEC,
∴DC=CE,
∴CE=OC,
∵∠OCE=30°,
∴∠COE=
(180°-30°)=75°.
∴∠DOC=∠AOB=60°,
∵四边形ABCD是矩形,
∴∠DCB=90°,AC=BD,AC=2CO,BD=2OD,
∴OC=OD,
∴△COD是等边三角形,
∴DC=OC,∠ACD=60°,
∴∠ACB=90°-60°=30°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠DEC,
∴DC=CE,
∴CE=OC,
∵∠OCE=30°,
∴∠COE=
| 1 |
| 2 |
点评:本题考查了矩形的性质,等边三角形的性质和判定,角平分线定义的应用,解此题的关键是求出OC=CE和求出∠ACB的度数,综合性比较强,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )
如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )| A、2 | B、4 | C、6 | D、8 |
 如果两个多边形的每个对应角相等,每条对应边成比例,那么我们就称这两个多边形相似,相似的两个矩形中心重合,如图放置在第一象限,他们的长(较长边)与宽(较短边)之比为k,且他们的长与宽分别与x轴和y轴平行,直线y=mx+n(m>0)分别交两个矩形的边于点P,Q,M,N,则线段PQ与MN之比为
如果两个多边形的每个对应角相等,每条对应边成比例,那么我们就称这两个多边形相似,相似的两个矩形中心重合,如图放置在第一象限,他们的长(较长边)与宽(较短边)之比为k,且他们的长与宽分别与x轴和y轴平行,直线y=mx+n(m>0)分别交两个矩形的边于点P,Q,M,N,则线段PQ与MN之比为 如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为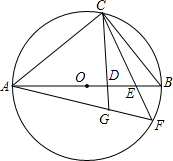 如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,
如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,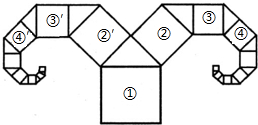 如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去…,若正方形①的面积为a,则正方形⑦的边长是多少?正方形
如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去…,若正方形①的面积为a,则正方形⑦的边长是多少?正方形 的边长是多少?
的边长是多少? 如图,⊙O是直径为4cm的圆形铁片,现用它截取最大的正方形ABCD.
如图,⊙O是直径为4cm的圆形铁片,现用它截取最大的正方形ABCD.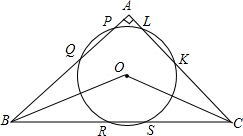 如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.
如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.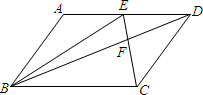 如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为
如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为