题目内容
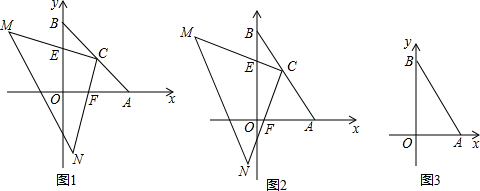
如图,以Rt△AOB的直角顶点O为坐标原点,OA所在直线为x轴,建立平面直角坐标系,C为AB的中点,将一个足够大的三角板的直角顶点与C重合,并绕点C旋转,直角边CM、CN与边OB、OA相交于E、F.
(1)如图1,当∠ABO=45°时,请直接写出线段CE与CF的数量关系: .
(2)如图2,当∠ABO=30°时,请直接写出CE与CF的数量关系: .
(3)当∠ABO=α时,猜想CE与CF的数量关系(用含有α的式子表示),并结合图2证明你的猜想.
(4)若OA=6,OB=8,D为△AOB的内心,结合图3,判断D是否在双曲线y=
上,说明理由.
(1)如图1,当∠ABO=45°时,请直接写出线段CE与CF的数量关系:
(2)如图2,当∠ABO=30°时,请直接写出CE与CF的数量关系:
(3)当∠ABO=α时,猜想CE与CF的数量关系(用含有α的式子表示),并结合图2证明你的猜想.
(4)若OA=6,OB=8,D为△AOB的内心,结合图3,判断D是否在双曲线y=
| 3 |
| x |

考点:反比例函数综合题
专题:
分析:(1)如图1,连接OC,易得四边形OFCE共圆,利用∠ABO=45°,C为AB的中点,可得∠EOC=∠FOC=45°,即可得出CE=CF,
(2)如图2,连接OC,易得四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,由∠ABO=30°,C为AB的中点,可得∠BOC=30°,∠FOC=60°,可得∠FGP=60°,所以FC=2FP=
r,同理可得EC=r,即可得FC=
EC.
(3)如图2,连接OC,易得四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,由∠ABO=α,C为AB的中点,可得∠BOC=α,∠FOC=90°-α,可得∠FGP=90°-α,所以FC=2FP=2rsin(90°-α),同理可得EC=2rsinα,可得FC:EC=sin(90°-α):sinα,即可求出FC与EC的关系.
(4)利用勾股定理求出AB的值,设OC为x,AC=6-x,由D为△AOB的内心,可得OE=x,BE=8-x,列出方程8-x+6-x=10,解得x=2,可得出点D(2,2).代入双曲线y=
不成立,可得D不在双曲线y=
上.
(2)如图2,连接OC,易得四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,由∠ABO=30°,C为AB的中点,可得∠BOC=30°,∠FOC=60°,可得∠FGP=60°,所以FC=2FP=
| 3 |
| 3 |
(3)如图2,连接OC,易得四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,由∠ABO=α,C为AB的中点,可得∠BOC=α,∠FOC=90°-α,可得∠FGP=90°-α,所以FC=2FP=2rsin(90°-α),同理可得EC=2rsinα,可得FC:EC=sin(90°-α):sinα,即可求出FC与EC的关系.
(4)利用勾股定理求出AB的值,设OC为x,AC=6-x,由D为△AOB的内心,可得OE=x,BE=8-x,列出方程8-x+6-x=10,解得x=2,可得出点D(2,2).代入双曲线y=
| 3 |
| x |
| 3 |
| x |
解答:解:(1)如图1,连接OC,
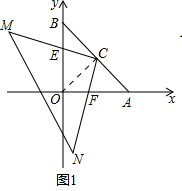
∵∠AOB=90°,∠MCN=90°,
∴四边形OFCE共圆,
∵∠ABO=45°,C为AB的中点,
∴∠EOC=∠FOC=45°,
∴CE=CF,
故答案为:CE=CF.
(2)如图2,连接OC,
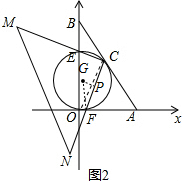
∵∠AOB=90°,∠MCN=90°,
∴四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,
∵∠ABO=30°,C为AB的中点,
∴∠BOC=30°,
∴∠FOC=60°,可得∠FGP=60°,
∴FC=2FP=
r,
同理可得EC=r,
∴FC=
EC.
故答案为:FC=
EC.
(3))如图2,连接OC,
∵∠AOB=90°,∠MCN=90°,
∴四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,
∵∠ABO=α,C为AB的中点,
∴∠BOC=α,
∴∠FOC=90°-α,可得∠FGP=90°-α,
∴FC=2FP=2rsin(90°-α),
同理可得EC=2rsinα,
∴FC:EC=sin(90°-α):sinα,
∴FC=
EC.
(4)如图3,
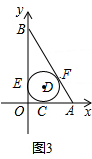
∵OA=6,OB=8,
∴AB=
=
=10,
设OC为x,AC=6-x,
∵D为△AOB的内心,
∴OE=x,BE=8-x,
∴8-x+6-x=10,
∴x=2,
∴点D(2,2).代入双曲线y=
不成立,
∴D不在双曲线y=
上,

∵∠AOB=90°,∠MCN=90°,
∴四边形OFCE共圆,
∵∠ABO=45°,C为AB的中点,
∴∠EOC=∠FOC=45°,
∴CE=CF,
故答案为:CE=CF.
(2)如图2,连接OC,

∵∠AOB=90°,∠MCN=90°,
∴四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,
∵∠ABO=30°,C为AB的中点,
∴∠BOC=30°,
∴∠FOC=60°,可得∠FGP=60°,
∴FC=2FP=
| 3 |
同理可得EC=r,
∴FC=
| 3 |
故答案为:FC=
| 3 |
(3))如图2,连接OC,
∵∠AOB=90°,∠MCN=90°,
∴四边形OFCE共圆,此圆为⊙G,设半径为r,作GP⊥FC,连接GF,
∵∠ABO=α,C为AB的中点,
∴∠BOC=α,
∴∠FOC=90°-α,可得∠FGP=90°-α,
∴FC=2FP=2rsin(90°-α),
同理可得EC=2rsinα,
∴FC:EC=sin(90°-α):sinα,
∴FC=
| sin(90°-α) |
| sinα |
(4)如图3,

∵OA=6,OB=8,
∴AB=
| OA2+OB2 |
| 62+82 |
设OC为x,AC=6-x,
∵D为△AOB的内心,
∴OE=x,BE=8-x,
∴8-x+6-x=10,
∴x=2,
∴点D(2,2).代入双曲线y=
| 3 |
| x |
∴D不在双曲线y=
| 3 |
| x |
点评:本题主要考查了反比例函数的综合题,涉及勾股定理,切线及共圆的知识,解题的关键是求出四边形OFCE共圆.

练习册系列答案
相关题目
 如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )
如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )| A、2 | B、4 | C、6 | D、8 |
 如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为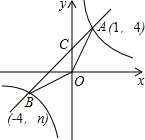 如图,已知:反比例函数y=
如图,已知:反比例函数y=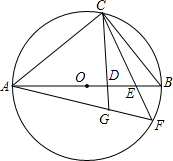 如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,
如图,已知AB是⊙O的直径,C为⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G, 如图,⊙O是直径为4cm的圆形铁片,现用它截取最大的正方形ABCD.
如图,⊙O是直径为4cm的圆形铁片,现用它截取最大的正方形ABCD.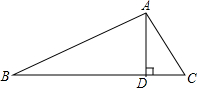 已知AB⊥AC于A,AD⊥BC于D,AB=8cm,AC=6cm,AD=4.8cm,BC=6.4cm,CD=3.6cm.
已知AB⊥AC于A,AD⊥BC于D,AB=8cm,AC=6cm,AD=4.8cm,BC=6.4cm,CD=3.6cm.