题目内容
已知正方形ABCD和正方形EBGF共顶点B,连AF,H为AF的中点,连EH,正方形EBGF绕点B旋转.
(1)如图1,当F点落在BC上时,求证:EH=
FC;
(2)如图2,当点E落在BC上时,连BH,若AB=5,BG=2,求BH的长;
(3)当正方形EBGF绕点B旋转到如图3的位置时,求
的值.

(1)如图1,当F点落在BC上时,求证:EH=
| 1 |
| 2 |
(2)如图2,当点E落在BC上时,连BH,若AB=5,BG=2,求BH的长;
(3)当正方形EBGF绕点B旋转到如图3的位置时,求
| EH |
| CF |

考点:几何变换综合题,全等三角形的判定与性质,等腰三角形的判定与性质,直角三角形斜边上的中线,勾股定理,三角形中位线定理,正方形的性质
专题:压轴题
分析:(1)延长FE交AB于点Q,易证EF=QE,QB=FB,从而可以证到HE=
AQ,AQ=CF,进而得到HE=
CF.
(2)延长EH交AB于点N,易证△ANH≌△FEH,则有NH=EH,AN=EF,进而可以证到BH=
EN,只需求出EN就可求出BH的值.
(3)过点A作EF平行线交EB的延长线于点T,延长EH交AT于S,连接SB、EC,易证△ASH≌△FEH,则有AS=EF,SH=EH.进而可以证到△SAB≌△EBC,则有SB=EC,∠ASB=∠BEC.由∠ASB=∠BEC可以推出∠SBE=∠CEF,从而可以证到△SBE≌△CEF,则有SE=CF,就可得到EH=
SE=
CF.
| 1 |
| 2 |
| 1 |
| 2 |
(2)延长EH交AB于点N,易证△ANH≌△FEH,则有NH=EH,AN=EF,进而可以证到BH=
| 1 |
| 2 |
(3)过点A作EF平行线交EB的延长线于点T,延长EH交AT于S,连接SB、EC,易证△ASH≌△FEH,则有AS=EF,SH=EH.进而可以证到△SAB≌△EBC,则有SB=EC,∠ASB=∠BEC.由∠ASB=∠BEC可以推出∠SBE=∠CEF,从而可以证到△SBE≌△CEF,则有SE=CF,就可得到EH=
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)证明:延长FE交AB于点Q,如图1,
解:(1)证明:延长FE交AB于点Q,如图1,
∵四边形EFBG是正方形,
∴EF=EB,∠EFB=∠EBF=45°.
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC.
∴∠BQF=∠QBE=45°.
∴QE=EB.
∴QE=EF.
∵AH=FH,
∴HE=
AQ.
∵∠BQF=∠BFQ=45°,
∴BQ=BF.
∵AB=BC,
∴AQ=CF.
∴HE=
CF.
(2) 延长EH交AB于点N,如图2,
延长EH交AB于点N,如图2,
∵四边形BEFG是正方形,
∴EF∥BG,EF=EB=BG=2.
∵EF∥AG,
∴∠FEH=∠ANH,∠EFH=∠NAH.
在△ANH和△FEH中,
∴△ANH≌△FEH.
∴NH=EH,AN=EF.
∵AB=5,AN=EF=2,
∴BN=AB-AN=3.
∵∠NBE=90°,BE=2,BN=3,
∴EN=
=
.
∵∠NBE=90°,EH=NH,
∴BH=
EN=
.
∴BH的值为
.
(3)过点A作EF平行线交EB的延长线于点T,
延长EH交AT于S,连接SB、EC,如图3,
∵EF∥AS,
∴∠FEH=∠ASH,∠EFH=∠SAH.
在△ASH和△FEH中,
∴△ASH≌△FEH.
∴AS=EF,SH=EH.
∵四边形BEFG是正方形,
∴BE=EF,∠FEB=90°.
∴AS=BE.
∵EF∥AS,
∴∠ATE=∠FEB=90°.
∴∠TAB+∠ABT=90°.
∵∠ABC=90°,
∴∠CBE+∠ABT=90°.
∴∠TAB=∠CBE.
在△SAB和△EBC中,
∴△SAB≌△EBC.
∴SB=EC.∠ASB=∠BEC.
∵∠ATB=90°,
∴∠TSB+∠TBS=90°.
∴∠ASB+∠SBE=360°-90°=270°.
∵∠BEC+∠CEF=360°-90°=270°,
∴∠SBE=∠CEF.
在△SBE和△CEF中,
.
∴△SBE≌△CEF.
∴SE=CF.
∵SH=EH,
∴EH=
SE=
CF.
∴
的值为
.
 解:(1)证明:延长FE交AB于点Q,如图1,
解:(1)证明:延长FE交AB于点Q,如图1,∵四边形EFBG是正方形,
∴EF=EB,∠EFB=∠EBF=45°.
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC.
∴∠BQF=∠QBE=45°.
∴QE=EB.
∴QE=EF.
∵AH=FH,
∴HE=
| 1 |
| 2 |
∵∠BQF=∠BFQ=45°,
∴BQ=BF.
∵AB=BC,
∴AQ=CF.
∴HE=
| 1 |
| 2 |
(2)
 延长EH交AB于点N,如图2,
延长EH交AB于点N,如图2,∵四边形BEFG是正方形,
∴EF∥BG,EF=EB=BG=2.
∵EF∥AG,
∴∠FEH=∠ANH,∠EFH=∠NAH.
在△ANH和△FEH中,
|
∴△ANH≌△FEH.
∴NH=EH,AN=EF.
∵AB=5,AN=EF=2,
∴BN=AB-AN=3.
∵∠NBE=90°,BE=2,BN=3,
∴EN=
| 22+32 |
| 13 |
∵∠NBE=90°,EH=NH,
∴BH=
| 1 |
| 2 |
| ||
| 2 |
∴BH的值为
| ||
| 2 |
(3)过点A作EF平行线交EB的延长线于点T,
延长EH交AT于S,连接SB、EC,如图3,
∵EF∥AS,
∴∠FEH=∠ASH,∠EFH=∠SAH.
在△ASH和△FEH中,
|
∴△ASH≌△FEH.
∴AS=EF,SH=EH.
∵四边形BEFG是正方形,
∴BE=EF,∠FEB=90°.
∴AS=BE.
∵EF∥AS,

∴∠ATE=∠FEB=90°.
∴∠TAB+∠ABT=90°.
∵∠ABC=90°,
∴∠CBE+∠ABT=90°.
∴∠TAB=∠CBE.
在△SAB和△EBC中,
|
∴△SAB≌△EBC.
∴SB=EC.∠ASB=∠BEC.
∵∠ATB=90°,
∴∠TSB+∠TBS=90°.
∴∠ASB+∠SBE=360°-90°=270°.
∵∠BEC+∠CEF=360°-90°=270°,
∴∠SBE=∠CEF.
在△SBE和△CEF中,
|
∴△SBE≌△CEF.
∴SE=CF.
∵SH=EH,
∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| EH |
| CF |
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、正方形的性质、三角形的中位线定理、勾股定理、直角三角形斜边上的中线等于斜边的一半等知识,综合性非常强,由一定的难度.而利用点H为AF的中点构造全等三角形是解决第三小题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(-3,0),B(0,-3)两点,二次函数y=x2+mx+n的图象经过点A.
在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(-3,0),B(0,-3)两点,二次函数y=x2+mx+n的图象经过点A.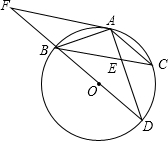 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.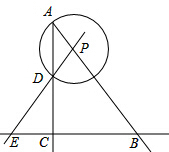 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E. 若在图中三顶点以外之18个圆圈内填入适当的数,使得任何一线段上相邻三个数均成等差,则位置A所填的数为
若在图中三顶点以外之18个圆圈内填入适当的数,使得任何一线段上相邻三个数均成等差,则位置A所填的数为