题目内容
已知一个三角形的三边长分别是7厘米,3厘米,第三边长为x厘米.
(1)求第三边x的取值范围;
(2)在(1)的条件下,取x的偶数值为直角△ABC的两直角边长(AC>BC),此时AB=10厘米,若P为斜边AB上的一个动点,求PC的最小值.
(1)求第三边x的取值范围;
(2)在(1)的条件下,取x的偶数值为直角△ABC的两直角边长(AC>BC),此时AB=10厘米,若P为斜边AB上的一个动点,求PC的最小值.
考点:勾股定理,垂线段最短,三角形三边关系
专题:
分析:(1)已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;
(2)根据(1)的条件下可得AC=8厘米,BC=6厘米,由勾股定理可知,
=10厘米,则AB是斜边,再根据三角形的面积公式即可得到PC的最小值.
(2)根据(1)的条件下可得AC=8厘米,BC=6厘米,由勾股定理可知,
| 82+62 |
解答:解:(1)根据三角形的三边关系,得
7-3<x<7+3,
即4<x<10.
(2)∵在(1)的条件下,取x的偶数值为直角△ABC的两直角边长(AC>BC),
∴AC=8厘米,BC=6厘米,
由勾股定理可知,
=10厘米,
∵AB=10厘米,
∴AB是斜边,
当PC⊥AB时,PC取最小值,
PC的最小值=
×8×6÷
÷10=4.8厘米,
故PC的最小值是4.8厘米.
7-3<x<7+3,
即4<x<10.
(2)∵在(1)的条件下,取x的偶数值为直角△ABC的两直角边长(AC>BC),
∴AC=8厘米,BC=6厘米,
由勾股定理可知,
| 82+62 |
∵AB=10厘米,
∴AB是斜边,
当PC⊥AB时,PC取最小值,
PC的最小值=
| 1 |
| 2 |
| 1 |
| 2 |
故PC的最小值是4.8厘米.
点评:考查了勾股定理,三角形三边关系,垂线段最短,本题需要理解的是如何根据已知的两条边求第三边的范围.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
若实数x满足x+
-1=0,则
的值为( )
| 2x |
| 3x2 |
| x4+x2+1 |
A、
| ||
B、
| ||
| C、5 | ||
D、
|
 在平面直角坐标系xOy中,点M(
在平面直角坐标系xOy中,点M(
 已知数a,b在数轴上的位置如图,化简
已知数a,b在数轴上的位置如图,化简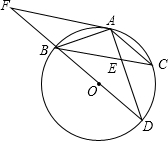 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.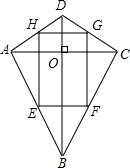 如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.
如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.