题目内容
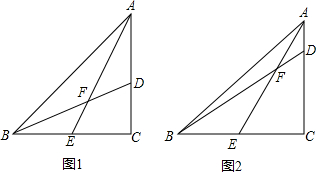 在△ABC中,AC=BC,∠ACB=90°,E是线段BC的中点,D在边AC上,线段BD和AE交于点F.
在△ABC中,AC=BC,∠ACB=90°,E是线段BC的中点,D在边AC上,线段BD和AE交于点F.(1)如图1,AD=CD时,求
| AE |
| AF |
(2)如图2,
| AD |
| AC |
| 1 |
| 4 |
考点:相似三角形的判定与性质,勾股定理
专题:常规题型
分析:(1)根据题意可以求得EF:AF的值,即可解题;
(2)作DG∥BC,EP⊥BD于P,可分别求得PF.PE的值,即可计算∠BFE的正切值.
(2)作DG∥BC,EP⊥BD于P,可分别求得PF.PE的值,即可计算∠BFE的正切值.
解答:解:(1)∵AD=CD,
∴D是AC的中点,
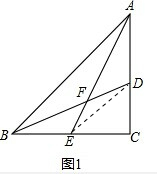
∴DE是△ACB的中位线,
=
,
∴
=
=
,
∴
=
;
(2)作DG∥BC,EP⊥BD于P,
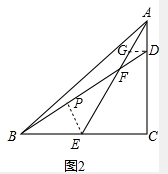
∵DG∥BC,
∴
=
=
,
∴
=
=
,
设AC=BC=4,则CD=3,
∴BD=
=5,
∴BF=
BD=4,
∵EP⊥BD,∴△BPE∽△BCD,
∴
=
=
,
∵BE=2,
∴BP=
,PE=
,
∴PF=BF-BP=4-
=
,
∴在RT△PEF中,tan∠BFE=
=
=
.
∴D是AC的中点,

∴DE是△ACB的中位线,
| DE |
| AB |
| 1 |
| 2 |
∴
| EF |
| AF |
| DE |
| AB |
| 1 |
| 2 |
∴
| AE |
| AF |
| 3 |
| 2 |
(2)作DG∥BC,EP⊥BD于P,

∵DG∥BC,
∴
| DG |
| EC |
| AD |
| AC |
| 1 |
| 4 |
∴
| DG |
| BE |
| 1 |
| 4 |
| DF |
| BF |
设AC=BC=4,则CD=3,
∴BD=
| BC2+CD2 |
∴BF=
| 4 |
| 5 |
∵EP⊥BD,∴△BPE∽△BCD,
∴
| BP |
| BE |
| BC |
| DB |
| 4 |
| 5 |
∵BE=2,
∴BP=
| 8 |
| 5 |
| 6 |
| 5 |
∴PF=BF-BP=4-
| 8 |
| 5 |
| 12 |
| 5 |
∴在RT△PEF中,tan∠BFE=
| PE |
| PF |
| ||
|
| 1 |
| 2 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比值相等的性质.

练习册系列答案
相关题目
-(-3)的倒数是( )
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
如果|a|=-a,下列成立的是( )
| A、a>0 |
| B、a<0 |
| C、a>0或a=0 |
| D、a<0或a=0 |
 已知,如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点.
已知,如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点.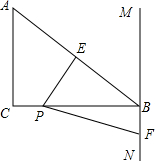 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作直线MN∥AC,点P在直线AC上,∠EPF=∠CAB,且两边分别交直线AB于E,交直线MN于F,如图,探究PE与PF之间的数量关系.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作直线MN∥AC,点P在直线AC上,∠EPF=∠CAB,且两边分别交直线AB于E,交直线MN于F,如图,探究PE与PF之间的数量关系.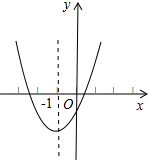 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果: