题目内容
6. 如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F.
如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F.(1)EF与AB之间有怎样的位置关系?为什么?
(2)EF,BC与AB之间有怎样的数量关系?为什么?
分析 (1)根据全等三角形的判定方法,结合题意可得△ADE≌△CBF;进而可得DE=BF,ED=EM;
(2)由(1)易得∠AMD=∠ABF,故EM∥BF进而可得根据平行线的性质可得EF=MB,BC=AD=AM,故有EF+BC=AB;
解答 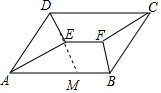 解:(1)EF∥AB,
解:(1)EF∥AB,
理由:延长DE交AB于M,
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,
∵DE,BF分别平分∠ADC,∠ABC,
∴∠CDE=$\frac{1}{2}∠$ADC,∠ABF=$\frac{1}{2}∠$ABC,
∴∠CDE=∠ABF,
∵AB∥CD,
∴∠CDM=∠AMD,
∴∠AMD=∠ABF,
∴EM∥BF,
∵∠ADC+∠BAD=180°,
∵AE、DE分别平分∠DAB和∠ADC
∴AE⊥DM,AE平分∠DAB.
∴ED=EM,
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∵AE、CF是角平分线.
∴∠DAE=∠BCF,
在△ADE与△CBF中,$\left\{\begin{array}{l}{∠DAE=∠BCF}\\{AD=BC}\\{∠ADE=∠CBF}\end{array}\right.$,
∴△ADE≌△CBF
∴DE=BF,ED=EM.
∴BF=EM,
∴四边形EMBF是平行四边形,
∴EF∥BM,
即EF∥AB;
(2)EF+BC=AB.
由(1)易证∠AMD=∠ABF,
∴EM∥BF,EM=BF.
∴四边形EFBM是平行四边形.
∴EF=MB,BC=AD=AM.
∴EF+BC=AB.
点评 本题考查的是平行四边形的性质和判定,角平分线的定义,平行线的判定,熟练掌握平行四边形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
15.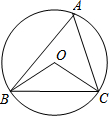 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 4 |
16.若直角三角形的两条直角边长分别是6和8,则它的外接圆半径为( )
| A. | $\sqrt{7}$ | B. | 4 | C. | 5 | D. | 10 |
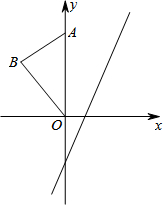 如图,点A的坐标为(0,6),将△OAB沿x轴向右平移得到△O'A'B',若点A的对应点A'落在直线y=2x-1上,则点B与其对应点间的距离为$\frac{7}{2}$.
如图,点A的坐标为(0,6),将△OAB沿x轴向右平移得到△O'A'B',若点A的对应点A'落在直线y=2x-1上,则点B与其对应点间的距离为$\frac{7}{2}$.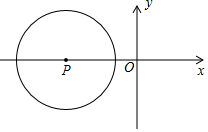 如图,在平面直角坐标系中,半径为2的圆P的圆心P的坐标为(-3,0),将圆P沿x轴的正方向平移,使得圆P与y轴相切,则平移的距离为( )
如图,在平面直角坐标系中,半径为2的圆P的圆心P的坐标为(-3,0),将圆P沿x轴的正方向平移,使得圆P与y轴相切,则平移的距离为( )