题目内容
14.如图1,Rt△ABC中,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P'),当AP旋转至AP'⊥AB时,点B、P、P'恰好在同一直线上,此时作P'E⊥AC于点E.(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8,求AE的长;
(3)当∠ABC=60°,BC=2,点N为BC的中点,在线段BP上确定点M,使MC+MN的值最小,利用图2,作出点M,并求出这个最小值.
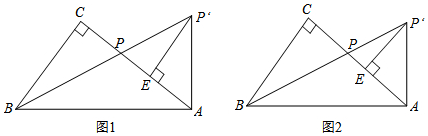
分析 (1)根据旋转的性质得到AP=AP',根据定义三角形的性质、三角形内角和定理计算即可;
(2)过点P作PD⊥AB于D,根据角平分线的性质得到CP=DP,证明△APD≌△P′AE,得到AE=DP,根据勾股定理求出AB、BC,计算即可;
(3)根据最短路径问题得到点C与点D关于BP对称,连接DN交BP于M,确定点M,根据正弦的定义求出ND即可.
解答 解:(1)∵AP=AP',
∴∠APP′=∠AP′P,
∵∠BCA=∠BAP′=90°,
∴∠BCA-∠BPC=∠BAP′-∠AP′P,即∠CBP=∠ABP;
(2)过点P作PD⊥AB于D,
∵∠CBP=∠ABP,∠C=90°,
∴CP=DP,
∵P′E⊥AC,
∴∠EAP′+∠AP′E=90°,
又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E,
在△APD和△P′AE中,
$\left\{\begin{array}{l}{∠PAD=∠AP′E}\\{∠ADP=∠P′EA}\\{AP=AP′}\end{array}\right.$,
∴△APD≌△P′AE(AAS),
∴AE=DP,
∴AE=CP,
∵AB-BC=4,AC=8,
∴AB=10,BC=6,
∴AE=CP=3;
(3)由题意得,点C与点D关于BP对称,
连接DN交BP于M,则点M即为所求,
∵∠ABC=60°,BD=BC=2,
∴MN+MC=ND=BD•sin∠ABC=$\sqrt{3}$,
∴MC+MN的值最小值为$\sqrt{3}$.
点评 本题考查的是全等三角形的判定和性质、最短路径问题,掌握全等三角形的判定定理和性质定理、正确确定点M的位置是解题的关键.

练习册系列答案
相关题目

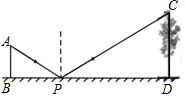 如图是小王同学设计的测量树高的示意图.在点P处放一水平的平面镜,小王同学站在地面的B处,通过平面镜刚好能看见大树CD的顶端C,若小王身高AB=1.6米,BP=3米,PD=15米,则大树的高度CD是8米.
如图是小王同学设计的测量树高的示意图.在点P处放一水平的平面镜,小王同学站在地面的B处,通过平面镜刚好能看见大树CD的顶端C,若小王身高AB=1.6米,BP=3米,PD=15米,则大树的高度CD是8米.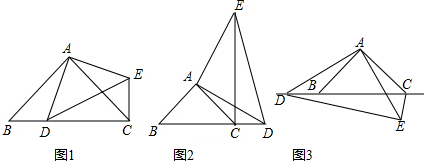
 在Rt△ABC中,∠ACB=90°,利用尺规在AC边上求作一点P,使PB+PC=AC,(保留作图痕迹,不写作法.)
在Rt△ABC中,∠ACB=90°,利用尺规在AC边上求作一点P,使PB+PC=AC,(保留作图痕迹,不写作法.)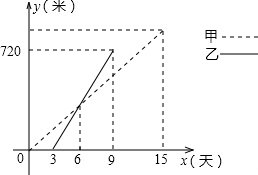 如皋某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
如皋某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
 如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8cm,ON=6cm.则该圆玻璃镜的直径是10cm.
如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8cm,ON=6cm.则该圆玻璃镜的直径是10cm.