题目内容
8．已知分式$\frac{x-3}{{x}^{2}-5x+a}$，当x=2时，分式无意义，则a=6；若对于任意x的值，分式均有意义，则a的取值范围是a＞$\frac{25}{4}$．分析 根据分母不为零分式有意义，可得答案．
解答 解：$\frac{x-3}{{x}^{2}-5x+a}$，当x=2时，分式无意义，得
22-5×2+a=0，解得a=6，
对于任意x的值，分式均有意义，得
（-5）2-4a＜0，
解得a＞$\frac{25}{4}$，
若对于任意x的值，分式均有意义，则a的取值范围是a＞$\frac{25}{4}$，
故答案为：6，a＞$\frac{25}{4}$．
点评 本题考查的是分式有意义的条件，熟知分式有意义的条件是分母不等于零是解答此题的关键．
练习册系列答案
相关题目
18．已知（2x-3y+1）2+|4x-3y-1|=0，则x，y的值分别为（ ）
| A． | -1，1 | B． | 1，-1 | C． | -1，-1 | D． | 1，1 |
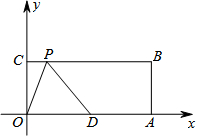已知，如图：在平面直角坐标系中，O为坐标原点，OABC是长方形，点A、C的坐标分别为A（20，0），C（0，8），点D是OA的中点，点P在BC边上运动，△ODP是腰长为10的等腰三角形时，求满足条件的点P点坐标．
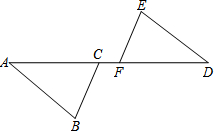已知：如图，AB∥DE，且AB=DE，AF=DC，求证：BC=EF．
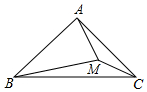如图，在△ABC中，∠BAC=90°，AB=AC，M为△ABC内一点，恰好满足BA=BM，AM=CM，则∠ABM的度数为30°．