题目内容
19．一直角三角形两直角边长的比是3：4，斜边长是20，那么这个直角三角形的面积是96．分析 根据两直角边之比设出两直角边，根据已知斜边，利用勾股定理求出两直角边，进而可求出其面积．
解答 解：根据题意设两直角边分别为3k，4k（k＞0），
由斜边为20，利用勾股定理得：9k2+16k2=400，即k2=16，
解得：k=4，
则两直角边分别为12和16，
所以这个直角三角形的面积=$\frac{1}{2}$×12×16=96，
故答案为：96．
点评 此题考查了勾股定理以及三角形面积公式的运用，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
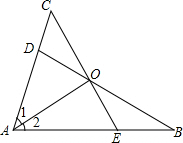已知：如图，点D、E分别在AC、AB上，BD、CE相交于点O，AC=AB，AD=AE，∠1=∠2，求证：
如图所示，有一个二级台阶，每一级的长宽、高分别为60cm、45cm、27cm，A和B是这两个台阶的相对端点，A点上有一只蚂蚁想到B点去吃可口的食物．若蚂蚁平均每秒走0.8cm，则蚂蚁沿着台阶从A到B至少需要多少时间？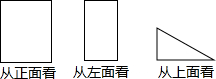
某几何体，从正面、左面和上面看到的物体形状如图所示．
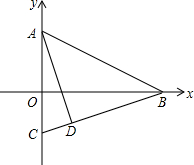如图，已知：直线y=-$\frac{1}{2}$x+3与y轴交于点A，与x轴交于点B，点C为y轴负半轴上一点，连接BC，且∠ABC=45°，BC=2$\sqrt{10}$，作AD⊥BC，垂足为D．
9．如果把多边形的边数增加一倍．得到的新多边形的内角和是1440°，那么原来多边形的边数是（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |