题目内容
16.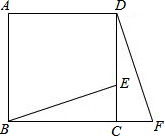 如图,E为正方形ABCD的边CD上一点,F为BC边延长线上一点,且有BE=DF,试判断BE与DF的位置关系.
如图,E为正方形ABCD的边CD上一点,F为BC边延长线上一点,且有BE=DF,试判断BE与DF的位置关系.
分析 由正方形的性质得出BC=CD、∠BCE=∠DCF=90°,由HL证明Rt△BCE≌Rt△DCF,得出∠1=∠2,由角的互余关系得出∠BMF=90°,得出BM⊥DF,即可得出结论.
解答 解:BE⊥DF,理由如下: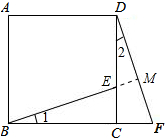
延长BE交DF于M,如图所示:
∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°,
∴∠DCF=90°,
在Rt△BCE和Rt△DCF中,$\left\{\begin{array}{l}{BE=DF}\\{BC=DC}\end{array}\right.$,
∴Rt△BCE≌Rt△DCF(HL),
∴∠1=∠2,
∵∠2+∠F=90°,
∴∠1+∠F=90°,
∴∠BMF=90°,
∴BM⊥DF,
即BE⊥DF.
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
 如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?