题目内容
2. 如图,斜坡AB的坡度为1:5,该段斜坡的长度为60m,求坡顶B点的垂直高度.
如图,斜坡AB的坡度为1:5,该段斜坡的长度为60m,求坡顶B点的垂直高度.
分析 由斜坡AB的坡度为1:5,根据坡度是坡面的铅直高度h和水平宽度l的比,可设BC=x,则AC=5x,利用勾股定理列出方程,解方程即可.
解答 解:在直角△ABC中,∵斜坡AB的坡度为1:5,
∴$\frac{BC}{AC}$=$\frac{1}{5}$,
∴可设BC=x,则AC=5x,
∵∠C=90°,AB=60,
∴BC2+AC2=AB2,
∴x2+(5x)2=602,
解得x=±$\frac{30\sqrt{26}}{13}$(负值舍去).
即坡顶B点的垂直高度是$\frac{30\sqrt{26}}{13}$m.
点评 此题考查了解直角三角形的应用-坡度坡角问题,勾股定理,坡度=坡角的正切值.掌握坡角与坡度的定义是解题的关键.坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式;把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h:l=tanα.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
12.一个多边形的内角和是1620°,那么这个多边形是( )
| A. | 八边形 | B. | 九边形 | C. | 十边形 | D. | 十一边形 |

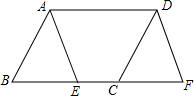 如图,在四边形ABCD中,AB=CD,AB∥CD,点E在边BC上,点F在BC的延长线上,且BE=CF,求证:△ABE≌△DCF.
如图,在四边形ABCD中,AB=CD,AB∥CD,点E在边BC上,点F在BC的延长线上,且BE=CF,求证:△ABE≌△DCF.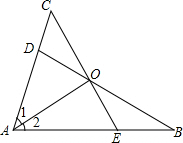 已知:如图,点D、E分别在AC、AB上,BD、CE相交于点O,AC=AB,AD=AE,∠1=∠2,求证:
已知:如图,点D、E分别在AC、AB上,BD、CE相交于点O,AC=AB,AD=AE,∠1=∠2,求证: 如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?