题目内容
17．求出代数式x2+2y2-6x+8y的最小值，并指出代数式最小时x，y的取值．分析 代数式配方变形后，利用非负数的性质求出最小值，以及此时x与y的值．
解答 解：∵x2+2y2-6x+8y=（x-3）2+2（y+2）2-17，
（x-3）2≥0，（y+2）2≥0，
∴x2+y2-6x+8y≥-17，
则当x=3，y=-2时，代数式取得最小值-17．
点评 此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
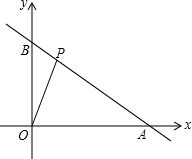直线y=kx+6与x轴、y轴分别交于A、B两点，点A的坐标为（8，0）．