题目内容
20．
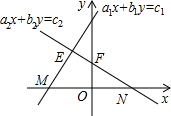如图，在平面直角坐标系xOy中，如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解，那么这个点是（ ）| A． | M | B． | N | C． | E | D． | F |
分析 本题可以通过直线与方程的关系得到两直线都过定点E，得到本题结论．
解答 解：两直线都过定点E，
所以点E表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解，
故选C
点评 本题考查的是直线与方程的关系，还可以用解方程组的方法加以解决．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
11．小明解方程组$\left\{\begin{array}{l}{3x+y=●}\\{3x-y=10}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=6}\\{y=★}\end{array}\right.$，由于不小心滴上了两滴墨水，刚好遮住了两个数●和★，则这两个数分别为（ ）
| A． | 26和8 | B． | -26和8 | C． | 8和-26 | D． | -26和5 |
8．
如图，△OAB与△OA′B′位似，其中A、B的对应点分别为A′，B′，A′，B′均在图中正方形网格格点上，若线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为（ ）
如图，△OAB与△OA′B′位似，其中A、B的对应点分别为A′，B′，A′，B′均在图中正方形网格格点上，若线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为（ ）| A． | （$\frac{m}{2}，\frac{n}{2}$） | B． | （m，n） | C． | （2m，2n） | D． | （2n，2m） |
如图，已知正方形ABCD的边长为1，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．
如图，正方形ABCD的面积是2，E，F，P分别是AB，BC，AC上的动点，PE+PF的最小值等于$\sqrt{2}$．