题目内容
9. 如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于$\sqrt{2}$.
如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于$\sqrt{2}$.
分析 过点P作MN∥AD交AB于点M,交CD于点N,根据正方形的性质可得出MN⊥AB,且PM≤PE、PN≤PF,由此即可得出AD≤PE+PF,再由正方形的面积为2即可得出结论.
解答 解:过点P作MN∥AD交AB于点M,交CD于点N,如图所示.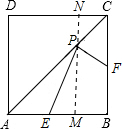
∵四边形ABCD为正方形,
∴MN⊥AB,
∴PM≤PE(当PE⊥AB时取等号),PN≤PF(当PF⊥BC时取等号),
∴MN=AD=PM+PN≤PE+PF,
∵正方形ABCD的面积是2,
∴AD=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了正方形的性质,解题的关键是找出AD≤PE+PF.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出PE+PF最小时,三点的位置关系是关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
17.用代入法解方程组$\left\{\begin{array}{l}{3x+4y=2①}\\{2x-y=5②}\end{array}\right.$,能使代入后化简比较容易的变形是( )
| A. | 由①得x=$\frac{2-4y}{3}$ | B. | 由①得y=$\frac{2-3x}{4}$ | C. | 由②得x=$\frac{5+y}{2}$ | D. | 由②得y=2x-5 |
4.若最简二次根式$\sqrt{7a+b}$与$\root{b+3}{6a-b}$可合并,则ab的值为( )
| A. | 2 | B. | -2 | C. | -1 | D. | 1 |
1.下列式子计算正确的是( )
| A. | a6÷b6=0 | B. | (-2a2)3=-6a6 | C. | (-a-b)2=a2-2ab+b2 | D. | (-a-b)(-a+b)=a2-b2 |
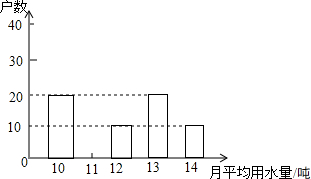 市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.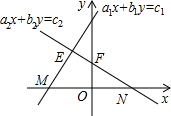 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )
如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )