题目内容
8. 如图,△OAB与△OA′B′位似,其中A、B的对应点分别为A′,B′,A′,B′均在图中正方形网格格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
如图,△OAB与△OA′B′位似,其中A、B的对应点分别为A′,B′,A′,B′均在图中正方形网格格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )| A. | ($\frac{m}{2},\frac{n}{2}$) | B. | (m,n) | C. | (2m,2n) | D. | (2n,2m) |
分析 根据A,B两点坐标以及对应点A′,B′点的坐标得出坐标变化规律,进而得出P′的坐标.
解答 解:∵△ABO扩大后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上,
即A点坐标为:(1,2),A′点坐标为:(2,4),
∴线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为:(2m,2n).
故选:C.
点评 此题主要考查了位似图形的性质,根据已知得出对应点坐标的变化是解题关键.

练习册系列答案
相关题目
16.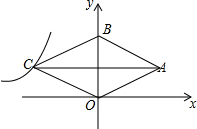 菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
 菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )| A. | 12 | B. | 24 | C. | -12 | D. | -24 |
3.下列方程的解为x=1的是( )
| A. | $\frac{x-1}{2}$=10 | B. | 2-x=2x-1 | C. | $\frac{2}{x}$+1=0 | D. | x2=2 |
13.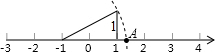 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )
 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )| A. | -$\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$+1 |
17.用代入法解方程组$\left\{\begin{array}{l}{3x+4y=2①}\\{2x-y=5②}\end{array}\right.$,能使代入后化简比较容易的变形是( )
| A. | 由①得x=$\frac{2-4y}{3}$ | B. | 由①得y=$\frac{2-3x}{4}$ | C. | 由②得x=$\frac{5+y}{2}$ | D. | 由②得y=2x-5 |
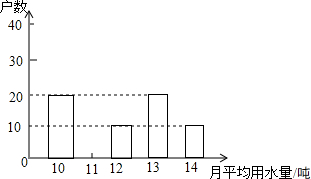 市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.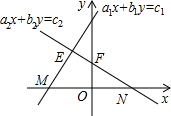 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )
如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )