题目内容
15.已知x=2+$\sqrt{3}$,y=2-$\sqrt{3}$,求下列各式的值:(1)x2+2xy+y2
(2)x2-y2.
分析 可先把所求的式子化成与x+y和x-y有关的式子,再代入求值即可.
解答 解:
∵x=2+$\sqrt{3}$,y=2-$\sqrt{3}$,
∴x+y=4,x-y=2$\sqrt{3}$,
(1)x2+2xy+y2=(x+y)2=42=16;
(2)x2-y2=(x+y)(x-y)=4×2$\sqrt{3}$=8$\sqrt{3}$.
点评 本题主要考查二次根式的化简,灵活运用乘法公式可以简化计算.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
3.下列方程的解为x=1的是( )
| A. | $\frac{x-1}{2}$=10 | B. | 2-x=2x-1 | C. | $\frac{2}{x}$+1=0 | D. | x2=2 |
7.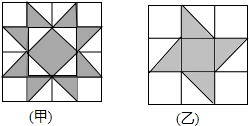 如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
 如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )| A. | P1<P2 | B. | P1=P2 | C. | P1>P2 | D. | 无法确定 |
4.若最简二次根式$\sqrt{7a+b}$与$\root{b+3}{6a-b}$可合并,则ab的值为( )
| A. | 2 | B. | -2 | C. | -1 | D. | 1 |
 如图,把△ABC向右平移4格,再向上平移2格得到△A′B′C′.请画出△A′B′C′.
如图,把△ABC向右平移4格,再向上平移2格得到△A′B′C′.请画出△A′B′C′.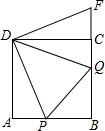 如图,在边长为8cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒3cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.
如图,在边长为8cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒3cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.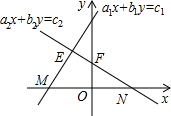 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )
如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解,那么这个点是( )