题目内容
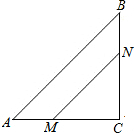 在△ABC中,∠C=90°,AC=16cm,BC=12cm,动点M、N分别从点A和点C同时开始移动,点M的速度为2cm/s,点N的速度为3m/s,点M移动到点C后停止,点N移动到点B后停止,问经过几秒,△MCN的面积为36cm2?
在△ABC中,∠C=90°,AC=16cm,BC=12cm,动点M、N分别从点A和点C同时开始移动,点M的速度为2cm/s,点N的速度为3m/s,点M移动到点C后停止,点N移动到点B后停止,问经过几秒,△MCN的面积为36cm2?考点:一元二次方程的应用
专题:几何动点问题
分析:设经过x秒,△MCN的面积为36cm2,利用路程=速度×时间知CM=(16-2x)cm,CN=3xcm,根据“△MCN的面积为36cm2”作为相等关系列方程求解即可.最后注意对根进行检验,舍去不合题意的值.
解答:解:设经过x秒,△MCN的面积为36cm2,依题意有
×3x(16-2x)=36,
解得x1=2,x2=6
经检验x2=6不符合题意,舍去.
则x=2.
答:经过2秒,△MCN的面积为36cm2.
| 1 |
| 2 |
解得x1=2,x2=6
经检验x2=6不符合题意,舍去.
则x=2.
答:经过2秒,△MCN的面积为36cm2.
点评:考查了一元二次方程的应用,此类题目要读懂题意,准确的找到等量关系列方程,解出方程的解后要注意代入实际问题中判断是否符合题意,进行值的取舍.

练习册系列答案
相关题目
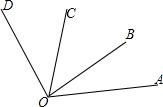 如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线?
如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线? 如图,一段长为1500m的水渠,其截面为等腰梯形ABCD,渠深AE=0.8m,底AB=1.2m,坡角为45°,那么该水渠最多能蓄水多少立方米?
如图,一段长为1500m的水渠,其截面为等腰梯形ABCD,渠深AE=0.8m,底AB=1.2m,坡角为45°,那么该水渠最多能蓄水多少立方米? 如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.