题目内容
在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,a=12,sinB=
,求b,c及∠A.(角度精确到1′)
| 4 |
| 5 |
考点:解直角三角形
专题:
分析:根据sinB=
可得b、c的大小关系,根据勾股定理即可求得b、c的值,即可解题.
| 4 |
| 5 |
解答:解:∵sinB=
=
,
∴b=
c,
∵a2+b2=c2,
∴c=20,b=16,
∴sinA=
=
,
∴∠A=36.87.
| b |
| c |
| 4 |
| 5 |
∴b=
| 4 |
| 5 |
∵a2+b2=c2,
∴c=20,b=16,
∴sinA=
| 12 |
| 20 |
| 3 |
| 5 |
∴∠A=36.87.
点评:本题考查了勾股定理在直角三角形中的运用,考查了直角三角形中三角函数值的计算,考查了计算器的使用,本题中求c的值是解题的关键.

练习册系列答案
相关题目
一元一次方程
+
+
+…+
=1025的解是( )
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 3×4 |
| x |
| 1025×1026 |
| A、1024 | B、1025 |
| C、1026 | D、1027 |
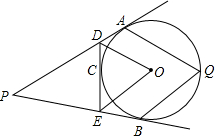 如图,从⊙O外一定点P作⊙O的两条切线,若C为
如图,从⊙O外一定点P作⊙O的两条切线,若C为
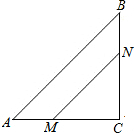 在△ABC中,∠C=90°,AC=16cm,BC=12cm,动点M、N分别从点A和点C同时开始移动,点M的速度为2cm/s,点N的速度为3m/s,点M移动到点C后停止,点N移动到点B后停止,问经过几秒,△MCN的面积为36cm2?
在△ABC中,∠C=90°,AC=16cm,BC=12cm,动点M、N分别从点A和点C同时开始移动,点M的速度为2cm/s,点N的速度为3m/s,点M移动到点C后停止,点N移动到点B后停止,问经过几秒,△MCN的面积为36cm2? 如图,求∠1+∠2的值.
如图,求∠1+∠2的值.