题目内容
 如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.(1)量一量∠D,∠F,∠B的度数,你能发现∠F与∠B,∠D之间有何等量关系吗?你能证明你所发现的结论吗?
(2)当∠B:∠D:∠F=2:4:x,你能运用你所发现的规律求x的值吗?试一试!
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)关系为∠D+∠B=2∠F,根据三角形内角和为180°的性质即可求证;
(2)根据∠B、∠D、∠F的比值,和(1)中结论即可求得x的值.
(2)根据∠B、∠D、∠F的比值,和(1)中结论即可求得x的值.
解答:(1)证明:∵CF平分∠BCD,EF平分∠BED
∴∠DEG=∠AEG,∠ACH=∠BCH,
∵在△DGE和△FGC中,∠DGE=∠FGC
∴∠D+∠DEG=∠F+∠ACH
∵在△BHC和△FHE中,∠BHC=∠FHE
∴∠B+∠BCH=∠F+∠AEG
∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG
∴∠D+∠B=2∠F;
(2)解:∵∠B:∠D:∠F=2:4:x,∠D+∠B=2∠F,
∴x=3.
∴∠DEG=∠AEG,∠ACH=∠BCH,
∵在△DGE和△FGC中,∠DGE=∠FGC
∴∠D+∠DEG=∠F+∠ACH
∵在△BHC和△FHE中,∠BHC=∠FHE
∴∠B+∠BCH=∠F+∠AEG
∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG
∴∠D+∠B=2∠F;
(2)解:∵∠B:∠D:∠F=2:4:x,∠D+∠B=2∠F,
∴x=3.
点评:本题考查了三角形内角和为180°的性质,本题中求∠D+∠B=2∠F是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
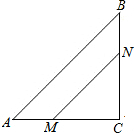 在△ABC中,∠C=90°,AC=16cm,BC=12cm,动点M、N分别从点A和点C同时开始移动,点M的速度为2cm/s,点N的速度为3m/s,点M移动到点C后停止,点N移动到点B后停止,问经过几秒,△MCN的面积为36cm2?
在△ABC中,∠C=90°,AC=16cm,BC=12cm,动点M、N分别从点A和点C同时开始移动,点M的速度为2cm/s,点N的速度为3m/s,点M移动到点C后停止,点N移动到点B后停止,问经过几秒,△MCN的面积为36cm2?
 如图,在Rt△ABC中,∠C=90°,BC=AC,D为AC的中点,求tan∠ABD的值.
如图,在Rt△ABC中,∠C=90°,BC=AC,D为AC的中点,求tan∠ABD的值. 如图,一个无盖的长方体长、宽、高分别为8cm、8cm、12cm,一只蚂蚁从A爬到C1,怎样爬路线最短,最短路径是多少?
如图,一个无盖的长方体长、宽、高分别为8cm、8cm、12cm,一只蚂蚁从A爬到C1,怎样爬路线最短,最短路径是多少?