题目内容
18.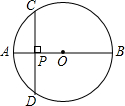 如图,⊙O中,CD为弦,AB为直径,CD⊥AB,垂足为P,AB=4,PA:PB=1:3,求PO和CD的长.
如图,⊙O中,CD为弦,AB为直径,CD⊥AB,垂足为P,AB=4,PA:PB=1:3,求PO和CD的长.
分析 根据已知求得PA=1,PB=3,OA=2,即可求得PO=1,由AB是直径,AB⊥CD所以利用垂径定理得到CP=PD,再利用相交弦定理就可以得到CP2=AP•BP,然后求出CD的长.
解答 解:∵AB为直径,CD⊥AB
∴PC=PD
∴CD=2PC,
∵AB=4,PA:PB=1:3,
∴PA=1,PB=3,OA=2,
∴PO=OA-PA=2-1=1,
由相交弦定理,得PC2=PA•PB=1×3=3,
∴PC=$\sqrt{3}$
∴CD=2$\sqrt{3}$.
点评 本题考查了垂径定理、相交弦定理的应用.熟练掌握这两个定理是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
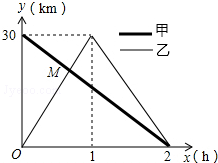 在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,下图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,下图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: