题目内容
16．在?ABCD中，AB=3，BC=4，AC=5，则?ABCD的面积为（ ）| A． | 6 | B． | 12 | C． | 18 | D． | 24 |
分析 由AB=3，BC=4，AC=5，由勾股定理的逆定理判定△ABC是直角三角形，得出四边形ABCD是矩形，继而求得?ABCD的面积．
解答 解：如图所示：
∵AB=3，BC=4，AC=5，
∴AB2+BC2=AC2，
∴∠ABC=90°，
∵四边形ABCD是平行四边形，
∴四边形ABCD是矩形，∴
∴S?ABCD=AB•BC=3×4=12．
故选：B．
点评 此题考查了平行四边形的性质、勾股定理的逆定理、矩形的判定；证得△ABC是直角三角形是解决问题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
7．
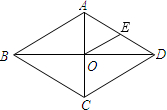如图，在菱形ABCD中，对角线AC、BD相交于点O，AC=6，BD=8，点E是AD边的中点，连接DE，则OE的长为（ ）
如图，在菱形ABCD中，对角线AC、BD相交于点O，AC=6，BD=8，点E是AD边的中点，连接DE，则OE的长为（ ）| A． | 10 | B． | $\frac{5}{2}$ | C． | 5 | D． | 4 |
4．
如图，函数y=3x和y=kx+3的图象相交于点A（m，2），则不等式3x＜kx+3的解集为（ ）
如图，函数y=3x和y=kx+3的图象相交于点A（m，2），则不等式3x＜kx+3的解集为（ ）| A． | x$＜\frac{2}{3}$ | B． | x$＞\frac{2}{3}$ | C． | x$＜\frac{3}{2}$ | D． | x$＞\frac{3}{2}$ |
11．
如图，已知AB∥CD，CF平分∠AFE，∠C=36°，则∠FED的度数是（ ）
如图，已知AB∥CD，CF平分∠AFE，∠C=36°，则∠FED的度数是（ ）| A． | 28° | B． | 56° | C． | 62° | D． | 72° |
1．从长度分别为2，4，6，8的四条线段中任选三条作边，能构成三角形的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
已知有理数a，b，c在数轴上的位置如图所示，化简|c-a|-|a+b|+|b-c|．