题目内容
 如图,点B、F、C、E在同一直线上,给出五个条件:
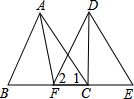
如图,点B、F、C、E在同一直线上,给出五个条件:①AB=DE;②BC=EF;③∠B=∠E;④∠1=∠2;⑤AF=CD.
请你从这五个条件中选出三个作为题设,一个作为结论,组成一个真命题,并给予证明.
考点:全等三角形的判定与性质,命题与定理
专题:开放型
分析:已知②③④,求证①,根据ASA推出△ABC≌△DEF,根据全等三角形的性质得出即可.
解答:条件是②③④,结论是①,
证明:∵在△ABC和△DEF中
∴△ABC≌△DEF(ASA),
∴AB=DE.
证明:∵在△ABC和△DEF中
|
∴△ABC≌△DEF(ASA),
∴AB=DE.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
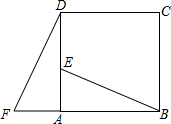 如图,在正方形ABCD中,E为AD的一点,F是BA延长线上的一点,DF=BE,判断AE与AF之间的数量关系.
如图,在正方形ABCD中,E为AD的一点,F是BA延长线上的一点,DF=BE,判断AE与AF之间的数量关系. 已知,如图,OE平分∠AOB,BC、AD分别垂直于OA、OB,求证:EC=DE.
已知,如图,OE平分∠AOB,BC、AD分别垂直于OA、OB,求证:EC=DE.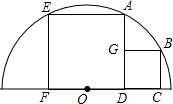 四边形ADFE和四边形BCDG都为正方形,且点F、D、C在半圆O的直径上,点E、A、B在半圆O的圆弧上,若小正方形边长为4cm,求该半圆的半径.
四边形ADFE和四边形BCDG都为正方形,且点F、D、C在半圆O的直径上,点E、A、B在半圆O的圆弧上,若小正方形边长为4cm,求该半圆的半径.