Question

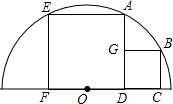四边形ADFE和四边形BCDG都为正方形，且点F、D、C在半圆O的直径上，点E、A、B在半圆O的圆弧上，若小正方形边长为4cm，求该半圆的半径．

Answer 1

考点：垂径定理,勾股定理,正方形的性质

专题：计算题

分析：先根据正方形的性质得EF=AD，则利用勾股定理可证明OD=OF，设OD=x，则OC=x+4，AD=2x，再根据勾股定理，在Rt△AOD中有OA²=OD²+AD²=5x²，
在Rt△OBC中有OB²=OC²+BC²=（x+4）²+4²，则（x+4）²+4²=5x²，然后解方程得到x=4，再利用OA=

5

x进行计算即可．

解答：解：连接OA、OB，如图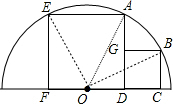
∵四边形AEDF为正方形，
∴EF=AD，
而OE=OA，OF=

OE2-EF2

，OD=

OA2-AD2

，
∴OD=OF，
设OD=x，则OC=x+4，AD=2x，
在Rt△AOD中，OA²=OD²+AD²=x²+（2x）²=5x²，
在Rt△OBC中，OB²=OC²+BC²=（x+4）²+4²，
而OA=OB，
∴（x+4）²+4²=5x²，
整理得x²-4x-8=0，解得x₁=4，x₂=-2（舍去），
∴OA=

5

x=4

5

，
即该半圆的半径为4

5

．

点评：本题主要考查了勾股定理的应用、一元二次方程的应用及正方形的性质，难度中等，是一道比较典型的圆的计算题．解答的关键是利用数形结合思想，设出适当的未知数，借助方程知识进行解答．