题目内容
已知等腰三角形的周长为24cm,腰长为x(cm),底边为y(cm),则底边y与x的函数关系式为 ,自变量x的取值范围是 .
考点:函数关系式,函数自变量的取值范围
专题:
分析:等腰三角形的两个腰是相等的,根据题中条件即可列出腰长和底边长的关系式.
解答:解:因为等腰三角形的两腰相等,周长为24,
所以2x+y=24,所以底边长y与腰长x的函数关系式为:y=-2x+24;
两边之和大于第三边,2x>y,
所以x>6,同时y>0,所以x<12,
所以x的取值范围是:6<x<12.
故答案为:y=-2x+24;6<x<12.
所以2x+y=24,所以底边长y与腰长x的函数关系式为:y=-2x+24;
两边之和大于第三边,2x>y,
所以x>6,同时y>0,所以x<12,
所以x的取值范围是:6<x<12.
故答案为:y=-2x+24;6<x<12.
点评:本题主要考查对于一次函数关系式的掌握以及三角形性质的应用,得出自变量取值范围是解题关键.

练习册系列答案
相关题目
化简
的结果是( )
| a-|a| |
| |a| |
| A、0或-2 | B、-2 |
| C、0或2 | D、2 |
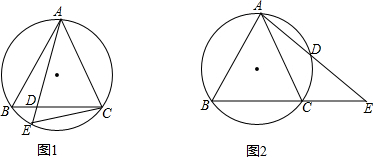
 由平面上一点A作⊙O的两条切线,切点分别为B,C.D为劣弧BC上任意一点,过D作AD的垂线交∠BOD和∠DOC的角平分线于点E和点F.求证:DE=DF.
由平面上一点A作⊙O的两条切线,切点分别为B,C.D为劣弧BC上任意一点,过D作AD的垂线交∠BOD和∠DOC的角平分线于点E和点F.求证:DE=DF. 如图,一货轮在B处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以30海里/时的速度沿北偏东45°方向航行,40分钟到达C处,此时又测得灯塔A在货轮的北偏西75°的方向上.
如图,一货轮在B处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以30海里/时的速度沿北偏东45°方向航行,40分钟到达C处,此时又测得灯塔A在货轮的北偏西75°的方向上.