题目内容
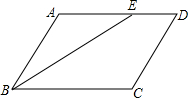 如图,在四边形ABCD中,已知BE平分∠ABC,交AD于E,∠AEB=∠ABE.
如图,在四边形ABCD中,已知BE平分∠ABC,交AD于E,∠AEB=∠ABE.(1)求证:AD∥BC;
(2)若AB∥CD,求证:∠D=2∠CBE.
考点:平行线的判定与性质
专题:证明题
分析:(1)证明∠AEB=∠CBE,即可解决问题.
(2)证明四边形ABCD为平行四边形,运用平行四边形的性质即可解决问题.
(2)证明四边形ABCD为平行四边形,运用平行四边形的性质即可解决问题.
解答: 解:(1)∵BE平分∠ABC,
解:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE,
又∵∠AEB=∠ABE.
∴∠AEB=∠CBE,
∴AD∥BC.
(2)∵AD∥BC,AB∥CD,
∴四边形ABCD为平行四边形,
∴∠D=∠ABC;
∵∠ABC=2∠CBE,
∴∠D=2∠CBE.
 解:(1)∵BE平分∠ABC,
解:(1)∵BE平分∠ABC,∴∠ABE=∠CBE,
又∵∠AEB=∠ABE.
∴∠AEB=∠CBE,
∴AD∥BC.
(2)∵AD∥BC,AB∥CD,
∴四边形ABCD为平行四边形,
∴∠D=∠ABC;
∵∠ABC=2∠CBE,
∴∠D=2∠CBE.
点评:该题主要考查了平行线的判定、平行四边形的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、解答;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
化简
的结果是( )
| a-|a| |
| |a| |
| A、0或-2 | B、-2 |
| C、0或2 | D、2 |
 如图,已知数轴上A、B、C、D四点对应的实数都是整数,且AB=CD=2BC,若A对应的有理数为a,B对应的有理数为b,且b-2a=7,则数轴上的原点是( )
如图,已知数轴上A、B、C、D四点对应的实数都是整数,且AB=CD=2BC,若A对应的有理数为a,B对应的有理数为b,且b-2a=7,则数轴上的原点是( ) 如图所示,OE为∠AOD的平分线,∠COD=
如图所示,OE为∠AOD的平分线,∠COD=