题目内容
5.在矩形ABCD中,对角线AC,BD相交于O,OF⊥AB于点F.若AC=2AD,OF=9cm,那么BD的长为36.分析 由矩形的性质得出AC=BD,OA=OB,由等腰三角形的三线合一性质得出AF=BF,证出OF是△ABD的中位线,由三角形中位线定理得出AD=2OF=18,求出AC,即可得出BD的长.
解答 解:如图所示: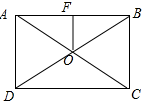
∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵OF⊥AB,
∴AF=BF,
∴OF是△ABD的中位线,
∴AD=2OF=18,
∴AC=2AD=36,
∴BD=36.
故答案为:36.
点评 本题考查了矩形的性质、三角形中位线定理;熟练掌握矩形的性质,由三角形中位线定理得出AD的长是解决问题的关键.

练习册系列答案
相关题目
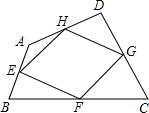 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个与四边形ABCD对角线有关的条件,为AC⊥BD,使四边形EFGH是矩形.
如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个与四边形ABCD对角线有关的条件,为AC⊥BD,使四边形EFGH是矩形.