题目内容
13.化简:(1)$\sqrt{(-121)×(-196)}$
(2)-$\frac{1}{3}$$\sqrt{(-9)^{2}}$
(3)-$\frac{1}{2}$$\sqrt{\frac{32}{75}}$
(4)$\sqrt{25{m}^{2}n}$(m<0)
分析 (1)根据二次根式的性质化简,即可解答.
(2)根据二次根式的性质化简,即可解答.
(3)根据二次根式的性质化简,即可解答.
(4)根据二次根式的性质化简,即可解答.
解答 解:(1)原式=$\sqrt{121×196}=\sqrt{121}×\sqrt{196}=11×14$=154.
(2)原式=$-\frac{1}{3}×\sqrt{{9}^{2}}=-\frac{1}{3}×9$=-3.
(3)原式=$-\frac{1}{2}×\frac{4\sqrt{6}}{15}=-\frac{2\sqrt{6}}{15}$.
(4)原式=-5$\sqrt{n}$.
点评 本题考查了二次根式的性质与化简,解决本题的关键是熟记二次根式的性质.

练习册系列答案
相关题目
3.已知:2m+3n=5,则4m•8n=( )
| A. | 16 | B. | 25 | C. | 32 | D. | 64 |
4.计算:(-2a)2•(-3a)3的结果是( )
| A. | -108a5 | B. | -108a6 | C. | 108a5 | D. | 108a6 |
 如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.
如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.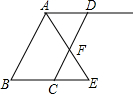 如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.
如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.