��Ŀ����
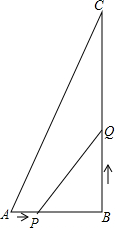 ��ͼ��ʾ���ڡ�ABC�У���B=90�㣬��ABC���߳�Ϊ��������ֱ�DZߵij�Ϊ����x��һԪ���η���x2-7x+��2k+8��=0����ʵ����������kΪ����������AB��BC��
��ͼ��ʾ���ڡ�ABC�У���B=90�㣬��ABC���߳�Ϊ��������ֱ�DZߵij�Ϊ����x��һԪ���η���x2-7x+��2k+8��=0����ʵ����������kΪ����������AB��BC����1�����ABC�����߳���
��2����P��A�㿪ʼ��AB�����B��1����λ��/����ٶ��ƶ�������Q��B�㿪ʼ��BC����C��2����λ��/����ٶ��ƶ������P��Q�ֱ��A��Bͬʱ���������������ӣ���PBQ�����Ϊ��ABC�����
| 1 |
| 3 |
���㣺һԪ���η��̵�Ӧ��
ר�⣺���ζ�������
��������1���������ø����б�ʽ���k��ȡֵ��Χ�������ֱ�ó����������ֵ��
��2�����������ʾ����PBQ������͡�ABC������������ó���ʽ������ɣ�
��2�����������ʾ����PBQ������͡�ABC������������ó���ʽ������ɣ�
����⣺��1���ߡ�=49-4��2k+8����0��
��ã�k��2
��
��k��������
��k=1��2��
��k=1ʱ��x2-7x+10=0��
��ã�x1=2��x2=5��
��ʱAC��Ϊ����������ȥ��
��k=2ʱ��x2-7x+12=0��
��ã�x1=3��x2=4��
��AB=3��BC=4����AC=5��
��2���辭��t���ӣ���PBQ�����Ϊ��ABC�����
��
��2t��3-t����
=
��
��3��4��
��ã�t1=1��t2=2��0��t��2��
��t=1��2��ʱ����PBQ�����Ϊ��ABC�����
��
��ã�k��2
| 1 |
| 8 |
��k��������
��k=1��2��
��k=1ʱ��x2-7x+10=0��
��ã�x1=2��x2=5��
��ʱAC��Ϊ����������ȥ��
��k=2ʱ��x2-7x+12=0��
��ã�x1=3��x2=4��
��AB=3��BC=4����AC=5��
��2���辭��t���ӣ���PBQ�����Ϊ��ABC�����
| 1 |
| 3 |
��2t��3-t����
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
��ã�t1=1��t2=2��0��t��2��
��t=1��2��ʱ����PBQ�����Ϊ��ABC�����
| 1 |
| 3 |
������������Ҫ������һԪ���η��̵�Ӧ�ã����������ʾ������������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
��������y=x2����ƽ��6����λ��������ƽ��8����λ���������Ϊ��������
| A��y=��x+6��2-8 |
| B��y=��x-6��2+8 |
| C��y=��x-6��2-8 |
| D��y=��x+6��2+8 |
���������У���ȷ���ǣ�������
�ٶ�����Բ���ϵĽ���Բ�ܽǣ���90���Բ�ܽ����Ե�����ֱ������Բ�ܽǶ�������Բ�ĽǶ�����һ�룻������ȷ��һ��Բ����ͬ�����Ե�Բ�ܽ���ȣ�
�ٶ�����Բ���ϵĽ���Բ�ܽǣ���90���Բ�ܽ����Ե�����ֱ������Բ�ܽǶ�������Բ�ĽǶ�����һ�룻������ȷ��һ��Բ����ͬ�����Ե�Բ�ܽ���ȣ�
| A���٢ڢ� | B���ۢܢ� |
| C���ڢ� | D���ڢ� |
��ͬһ����ϵ�У�������y=x2��y=-x2��y=
x2�Ĺ�ͬ���ǣ�������
| 1 |
| 2 |
| A���������ϣ��Գ�����y�ᣬ������ԭ�� |
| B���Գ�����y�ᣬ������ԭ�� |
| C���������£��Գ�����y�ᣬ������ԭ�� |
| D������СֵΪ0 |
�����к����У����ڶ��κ������ǣ�������
A��y=
| ||
B��y=x2+
| ||
| C��y=2x2-1 | ||
D��y=
|
 Сè��������ͼ��ʾ��ͼ���ϣ���ABC�����������������У�Сèͣ���ڰ�ש�ϵĸ���Ϊ
Сè��������ͼ��ʾ��ͼ���ϣ���ABC�����������������У�Сèͣ���ڰ�ש�ϵĸ���Ϊ ij���չ�˾�涨���˿���Я�����������x��kg�����˷�y��Ԫ��������ͼ��ʾ�ĺ���ͼ����ôÿλ�˿��������Я��
ij���չ�˾�涨���˿���Я�����������x��kg�����˷�y��Ԫ��������ͼ��ʾ�ĺ���ͼ����ôÿλ�˿��������Я��