题目内容
19．
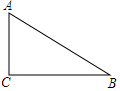如图，在△ABC中，∠C=90°，AC=3，BC=4，以点A为圆心，4为半径作⊙A，则（ ）| A． | 点B在⊙A外 | B． | 点B在⊙A上 | ||
| C． | 点B在⊙A外内 | D． | 点B与⊙A的位置关系不能确定 |
分析 根据勾股定理求出AB的值，根据点与圆的位关系特点，判断即可．
解答 解：由勾股定理得：AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∵以点A为圆心，4为半径作⊙A，5＞4，
∴点B在⊙A外，
故选A．
点评 本题考查了点与圆的位置关系定理和勾股定理等知识点的应用，点与圆（圆的半径是r，点到圆心的距离是d）的位置关系有3种：d=r时，点在圆上；d＜r时，点在圆内；d＞r时，点在圆外．
练习册系列答案
相关题目
10．下列实数$\sqrt{2}$，-$\root{3}{4}$，0.$\stackrel{..}{32}$，$\frac{22}{7}$，$\frac{π}{3}$，（$\sqrt{2}$-1）0，-$\sqrt{9}$，0.1010010001…中，其中非无理数共有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
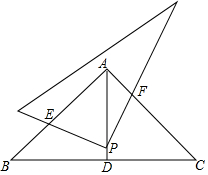如图，在△ABC中，∠BAC=90°，AB=AC，AD是斜边BC上的中线，将三角尺的直角顶点置于中线AD上点P处，三角尺的两条直角边分别交AB、AC边于点E、F．求证：PE=PF．