题目内容
20.计算(1)$\frac{x^2}{x-1}$-x-1
(2)先化简$\frac{2a+2}{a-1}÷(a+1)+\frac{{{a^2}-1}}{{{a^2}-2a+1}}$,然后a在-1、1、2三个数中任选一个合适的数代入求值.
分析 (1)先通分,然后计算;
(2)先化除法为乘法,然后利用提取公因式、完全平方公式、平方差公式进行因式分解,通过约分对已知分式进行化简,最后代入求值.
解答 解:(1)原式=$\frac{{x}^{2}-(x-1)(x+1)}{x-1}$=$\frac{{x}^{2}-{x}^{2}+1}{x-1}$=$\frac{1}{x-1}$;
(2)$\frac{2a+2}{a-1}÷(a+1)+\frac{{{a^2}-1}}{{{a^2}-2a+1}}$
=$\frac{2(a+1)}{a-1}$×$\frac{1}{a+1}$+$\frac{(a+1)(a-1)}{(a-1)^{2}}$
=$\frac{2}{a-1}$+$\frac{a+1}{a-1}$
=$\frac{a+3}{a-1}$,
当a=2时,原式=5.
点评 本题考查了分式的化简求值,分式的加减法.分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.就本节内容而言,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列多项式乘法中,能用平方差公式计算的是( )
| A. | (a+b2)(a2-b) | B. | (a+2)(2+a) | C. | (-a+b)(a-b) | D. | (2a+b)(-2a+b) |
9.若代数式5x2-4x+6的值为26,则${x^2}-\frac{4}{5}x+6$的值为( )
| A. | 6 | B. | 10 | C. | 14 | D. | 30 |

 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.求证:AF∥CE且AF=CE.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.求证:AF∥CE且AF=CE.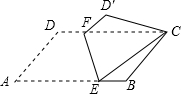 如图,将?ABCD折叠,使点A与C重合,折痕为EF.若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.
如图,将?ABCD折叠,使点A与C重合,折痕为EF.若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.