题目内容
10．已知a是方程x2+5x-2=0的一个根，则代数式2a2+10a-7的值为-3；代数式a3+6a2+3a+4的值为6．分析 根据一元二次方程的解的定义，将x=a代入方程x2+5x-2=0，求得代数式a2+5a的值即可．
解答 解：∵a是方程x2+5x-2=0的一个根，
∴x=a满足该方程，
∴a2+5a-2=0，
即a2+5a=2，
∴2a2+10a-7=2（a2+5a）-7=4-7=-3；
a3+6a2+3a+4=a（a2+5a）+a2+3a+4=a2+5a+4=2+4=6，
故答案为：-3，6．
点评 本题考查了一元二次方程的解、代数式求值．解答该题时，只要仔细观察代数式a2+5a与方程x2+5x=2的联系系，就很容易求得该代数式的值．
练习册系列答案
相关题目
1．下列算式中，正确的有（ ）
| A． | $\sqrt{3}$+$\sqrt{4}$=$\sqrt{7}$ | B． | 3$\sqrt{2}$-2$\sqrt{2}$=-$\sqrt{2}$ | C． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | D． | $\sqrt{1\frac{1}{2}}$÷$\sqrt{\frac{1}{6}}$=3 |
18．
如图，以正六边形ADHGFE的一边AD为边向外作正方形ABCD，则∠BED的度数为（ ）
如图，以正六边形ADHGFE的一边AD为边向外作正方形ABCD，则∠BED的度数为（ ）| A． | 30° | B． | 45° | C． | 50° | D． | 60° |
如图，在?ABCD中，∠ADC的角平分线DE交AC于点F，AE=2，则AD=2．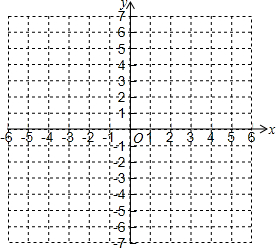
在平面直角坐标系中，描出下列3个点：A （-1，0），把点A向右平移2个单位，再向上平移4个单位得到点B，点C 的坐标是（4，2）； 
如图，一块平行四边形场地ABCD，测得∠ABC=60°，AB=2，AD=4，AE⊥BD于点E，CF⊥BD于点F，连接CE，AF．现计划在四边形AECF区域内种植花草．