题目内容
10.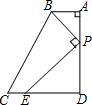 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E.
如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E.(1)求证:△ABP∽△DPE;
(2)设AP=x,DE=y,求y与x之间的函数关系式,并写出x的取值范围;
(3)请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由.
分析 (1)根据同角的余角相等得到∠ABP=∠EPD,根据相似三角形的判定定理证明结论;
(2)根据相似三角形的性质列出比例式,计算即可;
(3)根据矩形的判定定理、结合一元二次方程计算即可.
解答 (1)证明:∵∠A=90°,
∴∠ABP+∠APB=90°,
∵PE⊥BP,
∴∠EPD+∠APB=90°,
∴∠ABP=∠EPD,
∵AB∥CD,∠A=90°,
∴∠D=90°,
∴△ABP∽△DPE;
(2)∵△ABP∽△DPE,
∴$\frac{AB}{PD}$=$\frac{AP}{DE}$,即$\frac{2}{5-x}$=$\frac{x}{y}$,
则y=-$\frac{1}{2}$x2+$\frac{5}{2}$x,0<x<5;
(3)当四边形ABED为矩形时,DE=AB=2,即y=2,
则-$\frac{1}{2}$x2+$\frac{5}{2}$x=2,
解得,x1=1,x2=4(舍去),
∴当AP=1时,四边形ABED能构成矩形.
点评 本题考查的是相似三角形的判定和性质、矩形的判定和性质,掌握相关的性质定理和判断定理是解题的关键,注意函数思想在解题中的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列等式从左边到右边的变形属于分解因式的是( )
| A. | (2x+1)(2x-1)=4x2-1 | B. | 2x3-4x2=x2(2x-4) | C. | x2-4x+4=x(x-4)+4 | D. | x2+2x+1=(x+1)2 |
16.正比例函数y=kx(k>0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |