题目内容
1．数据：10，15，10，17，18，20的方差是$\frac{44}{3}$．分析 先由平均数的公式计算出平均数的值，再根据方差的公式计算．
解答 解：平均数=（10+15+10+17+18+20）÷6=15，
方差=$\frac{1}{6}$[2（10-15）2+（15-15）2+（17-15）2+（18-15）2+（20-15）2]=$\frac{44}{3}$．
故答案为：$\frac{44}{3}$．
点评 本题考查方差的定义：一般地设n个数据，x1，x2，…xn的平均数为$\overline{x}$，则方差S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
练习册系列答案
金博士一点全通系列答案
相关题目
11．下列各方程，变形不正确的是（ ）
| A． | $\frac{x-3}{5}-\frac{x+4}{2}=1$去分母化为2（x-3）-5（x+4）=10 | |
| B． | 2（x-3）-5（x+4）=10去括号为：2x-3-5x+20=10 | |
| C． | 2x-3-5x+20=10移项得：2x-5x=10-20+3 | |
| D． | 2x-5x=10-20+3合并同类项得：-3x=-7 |
12．
一副三角尺拼成如图所示的图案，则∠ABC的大小为（ ）
一副三角尺拼成如图所示的图案，则∠ABC的大小为（ ）| A． | 100° | B． | 110° | C． | 120° | D． | 135° |
如图，BD是△ABC的角平分线，DE⊥AB于点E．△ABC的面积为20，AB=12，BC=8，则DE的长为2．
6．方程x2-2（3x-2）=5的一般形式是（ ）
| A． | x2-6x+4=5 | B． | x2-6x-4=5 | C． | x2-6x-1=0 | D． | x2-6x-9=0 |
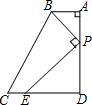如图，在四边形ABCD中，AB∥CD，∠A=90°，AB=2，AD=5，P是AD上一动点（点P不与A、D重合），PE⊥BP，PE交DC于点E．