题目内容
 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.(1)求证:BD=EC;
(2)若AC=2,sin∠E=
| 1 |
| 2 |
考点:菱形的性质,勾股定理,平行四边形的判定与性质
专题:
分析:(1)根据菱形的对边平行且相等可得AB=CD,AB∥CD,然后证明得到BE=CD,BE∥CD,从而证明四边形BECD是平行四边形,再根据平行四边形的对边相等即可得证;
(2)欲求菱形ABCD的面积,只需求得AC、BD的长度即可.利用平行四边形BECD的性质推知∠E=∠OBA,所以通过解直角△OBA和勾股定理易求OB的长度.则利用菱形ABCD的对角线互相平分易求BD的长度.
(2)欲求菱形ABCD的面积,只需求得AC、BD的长度即可.利用平行四边形BECD的性质推知∠E=∠OBA,所以通过解直角△OBA和勾股定理易求OB的长度.则利用菱形ABCD的对角线互相平分易求BD的长度.
解答:(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形,
∴BD=EC;
(2)解:∵四边形BECD是平行四边形,
∴DB∥CE,
∴∠E=∠OBA,
∴sin∠OBA=sin∠E=
.
∵四边形ABCD是菱形,
∴∠AOB=90°,OA=
AC=1,
∴sin∠OBA=
=
=
,
∴AB=2.
∴OB=
=
,
∴BD=2OB=2
,
∴S菱形ABCD=
AC•BD=
×2×2
=2
.
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形,
∴BD=EC;
(2)解:∵四边形BECD是平行四边形,
∴DB∥CE,
∴∠E=∠OBA,
∴sin∠OBA=sin∠E=
| 1 |
| 2 |
∵四边形ABCD是菱形,
∴∠AOB=90°,OA=
| 1 |
| 2 |
∴sin∠OBA=
| OA |
| AB |
| 1 |
| AB |
| 1 |
| 2 |
∴AB=2.
∴OB=
| AB2-OA2 |
| 3 |
∴BD=2OB=2
| 3 |
∴S菱形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题综合考查了菱形的性质,平行四边形的判定与性质以及勾股定理.解(2)题时,主要利用菱形的对角线互相垂直平分及勾股定理来解决.

练习册系列答案
相关题目
 已知实数m、n在数轴上的对应点的位置如图,则|m-n|+
已知实数m、n在数轴上的对应点的位置如图,则|m-n|+| (n-1)2 |
| A、m-1 | B、m+1 |
| C、2n-m+1 | D、2n-m-1 |
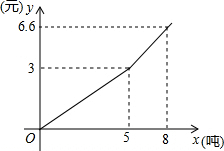 某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题:
某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题: 如图,如果把四边形ABCD沿EF折叠,使点A,B落在四边形EFCD内,试探究∠A+∠B与∠1+∠2之间存在着怎样的数量关系,证明你的结论.
如图,如果把四边形ABCD沿EF折叠,使点A,B落在四边形EFCD内,试探究∠A+∠B与∠1+∠2之间存在着怎样的数量关系,证明你的结论.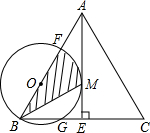 如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.