题目内容
12.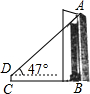 如图,为了解测量长春解放纪念碑的高度AB,在与纪念碑底部B相距27米的C处,用高1.5米的测角仪DC测得纪念碑顶端A的仰角为47°,求纪念碑的高度(结果精确到0.1米)
如图,为了解测量长春解放纪念碑的高度AB,在与纪念碑底部B相距27米的C处,用高1.5米的测角仪DC测得纪念碑顶端A的仰角为47°,求纪念碑的高度(结果精确到0.1米)【参考数据:sin47°=0.731,cos47°=0.682,tan47°=1.072】
分析 作DE⊥AB于E,根据正切的概念求出AE的长,再结合图形根据线段的和差计算即可求解.
解答  解:作DE⊥AB于E,
解:作DE⊥AB于E,
由题意得DE=BC=27米,∠ADE=47°,
在Rt△ADE中,AE=DE•tan∠ADE=27×1.072=28.944米,
AB=AE+BE≈30.4米,
答:纪念碑的高度约为30.4米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
2.若顺次连结四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必定是( )
| A. | 菱形 | B. | 对角线相互垂直的四边形 | ||
| C. | 正方形 | D. | 对角线相等的四边形 |
3.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. | 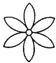 | C. | 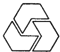 | D. |  |
7. 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )| A. | 42° | B. | 48° | C. | 52° | D. | 58° |
4.一元二次方程x2-4x+4=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
13.0.1252016×(-8)2016的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | $\frac{1}{4}$ |
14.平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为( )
| A. | 1<AB<2 | B. | 2<AB<10 | C. | 4<AB<10 | D. | 4<AB<20 |
 如图是由4个大小相同的小立方块搭成的几何体,这个几何体的俯视图是( )
如图是由4个大小相同的小立方块搭成的几何体,这个几何体的俯视图是( )


