题目内容
14.平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为( )| A. | 1<AB<2 | B. | 2<AB<10 | C. | 4<AB<10 | D. | 4<AB<20 |
分析 根据平行四边形的性质求出OA和OB,在△AOB中,根据三角形三边关系定理得出6-4<AB<6+4,即可得出结果.
解答  解:如图所示:
解:如图所示:
∵四边形ABCD是平行四边形,AC=12,BD=8,
∴OA=OC=6,OB=OD=4,
在△AOB中,由三角形三边关系定理得:6-4<AB<6+4,
即2<AB<10,
故选:B.
点评 本题考查了三角形的三边关系定理和平行四边形的性质,注意:平行四边形的对角线互相平分.

练习册系列答案
相关题目
2.等腰直角三角形三边长度之比为( )
| A. | 1:1:2 | B. | 1:1:$\sqrt{2}$ | C. | 1:2:$\sqrt{3}$ | D. | 不能确定 |
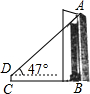 如图,为了解测量长春解放纪念碑的高度AB,在与纪念碑底部B相距27米的C处,用高1.5米的测角仪DC测得纪念碑顶端A的仰角为47°,求纪念碑的高度(结果精确到0.1米)
如图,为了解测量长春解放纪念碑的高度AB,在与纪念碑底部B相距27米的C处,用高1.5米的测角仪DC测得纪念碑顶端A的仰角为47°,求纪念碑的高度(结果精确到0.1米)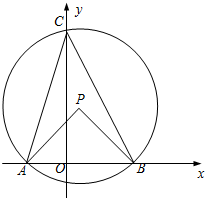 已知如图,圆P经过点A(-4,0),点B(6,0),交y轴于点C,∠ACB=45°,连结AP、BP.
已知如图,圆P经过点A(-4,0),点B(6,0),交y轴于点C,∠ACB=45°,连结AP、BP. 如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.
如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.