题目内容
2.若顺次连结四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必定是( )| A. | 菱形 | B. | 对角线相互垂直的四边形 | ||
| C. | 正方形 | D. | 对角线相等的四边形 |
分析 根据矩形的四个角为直角得到∠FEH=90°,又EF为三角形ABD的中位线,根据中位线定理得到EF与DB平行,根据两直线平行,同旁内角互补得到∠EMO=90°,同理根据三角形中位线定理得到EH与AC平行,再根据两直线平行,同旁内角互补得到∠AOD=90°,根据垂直定义得到AC与BD垂直.
解答 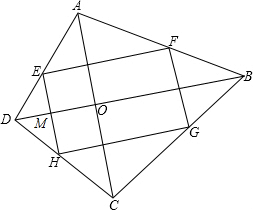 解:∵四边形EFGH是矩形,
解:∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故选:B.
点评 此题考查了矩形的性质,三角形的中位线定理,以及平行线的性质.这类题的一般解法是:借助图形,充分抓住已知条件,找准问题的突破口,由浅入深多角度,多侧面探寻,联想符合题设的有关知识,合理组合发现的新结论,围绕所探结论环环相加,步步逼近,所探结论便会被“逼出来”.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.命题甲:由正比例函数图象上任意一点的坐标可以确定该正比例函数的解析式;
命题乙:大边上的中线等于大边一半的三角形是直角三角形.
则下列判断正确的是( )
命题乙:大边上的中线等于大边一半的三角形是直角三角形.
则下列判断正确的是( )
| A. | 两命题都正确 | B. | 两命题都不正确 | C. | 甲不正确乙正确 | D. | 甲正确乙不正确 |
10.在平面直角坐标系中,点A(7,-2)关于x轴对称的点A′的坐标是( )
| A. | (7,2) | B. | (7,-2) | C. | (-7,2) | D. | (-7,-2) |
17.关于反比例函数$y=\frac{2}{x}$的图象,下列叙述错误的是( )
| A. | y随x的增大而减小 | B. | 图象位于一、三象限 | ||
| C. | 图象关于原点对称 | D. | 点(-1,-2)在这个图象上 |
14.如果y关于x的函数y=(k2+1)x是正比例函数,那么k的取值范围是( )
| A. | k≠0 | B. | k≠±1 | C. | 一切实数 | D. | 不能确定 |




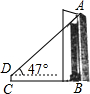 如图,为了解测量长春解放纪念碑的高度AB,在与纪念碑底部B相距27米的C处,用高1.5米的测角仪DC测得纪念碑顶端A的仰角为47°,求纪念碑的高度(结果精确到0.1米)
如图,为了解测量长春解放纪念碑的高度AB,在与纪念碑底部B相距27米的C处,用高1.5米的测角仪DC测得纪念碑顶端A的仰角为47°,求纪念碑的高度(结果精确到0.1米)