题目内容
1．菱形的两条对角线长分别是方程x2-14x+48=0的两实根，则菱形的面积为（ ）| A． | 48 | B． | 25 | C． | 24 | D． | 12 |
分析 解一元二次方程x2-14x+48=0，求出它的两个实数根，即菱形两条对角线的长，利用菱形的对角线互相垂直性质，计算出菱形的面积．
解答 解：（法一）由x2-14x+48=0，
得（x-6）（x-8）=0
∴x1=6，x2=8
即菱形两条对角线的长分别为6和8，
所以S菱形=$\frac{1}{2}$×6×8=24．
故选C．
（法二）设菱形的两条边分别长为a、b．
由于a、b是方程x2-14x+48=0的两实恨，
所以ab=48，
所以S菱形=$\frac{1}{2}$×48=24．
故选C．
点评 本题考查了一元二次方程的解法、一元二次方程根与系数的关系及菱形的面积公式．菱形的面积有两种计算办法：1．S菱形=$\frac{1}{2}$底边×该底边上的高；2．S菱形=$\frac{1}{2}$×对角线长的积．
练习册系列答案
相关题目
9．下列各命题都成立，其中逆命题也成立的是（ ）
| A． | 若a＞0，b＞0，则a+b＞0 | B． | 对顶角相等 | ||
| C． | 全等三角形的对应角相等 | D． | 平行四边形的两组对边分别相等 |
16．将长度为6cm的线段向上平移8cm再向右平移6cm，所得线段长为（ ）
| A． | 12cm | B． | 10cm | C． | 6cm | D． | 无法确定 |
13．
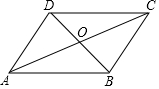如图，已知AC、BD相交于点O，AO=CO，BO=DO，则图中能判定全等的三角形有（ ）
如图，已知AC、BD相交于点O，AO=CO，BO=DO，则图中能判定全等的三角形有（ ）| A． | 1对 | B． | 2对 | C． | 3对 | D． | 4对 |
10．如果3xm+2y3与-2x3y2n-1是同类项，则m、n的值分别是（ ）
| A． | m=1，n=2 | B． | m=0，n=2 | C． | m=2，n=1 | D． | m=1，n=1 |
