题目内容
抛物线y=-2（x+1）2+3的开口方向是 ，对称轴是 ，顶点坐标是 ．
考点：二次函数的性质
专题：
分析：已知抛物线解析式为顶点式，可根据顶点式求抛物线的开口方向，对称轴及顶点坐标．
解答：解：∵y=-2（x+1）2+3，二次项系数为-2＜0，
∴抛物线开口向下，对称轴为直线x=-1，顶点坐标为（-1，3）．
故本题答案为：向下，x=-1，（-1，3）．
∴抛物线开口向下，对称轴为直线x=-1，顶点坐标为（-1，3）．
故本题答案为：向下，x=-1，（-1，3）．
点评：本题考查了二次函数解析式的顶点式与其性质的联系，根据二次项系数的符号确定开口方向，根据顶点式确定顶点坐标及对称轴．
练习册系列答案
相关题目
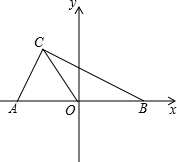如图在平面直角坐标系中，A（a，0），B（b，0），（-1，2）．且|2a+b+1|+
如图，AB⊥CD，垂足为B，EF是过点B的一条直线，已知∠EBD=135°，则∠CBE=在△ABC中，∠C=90°，已知tanA=
，则cosB的值等于（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|