题目内容
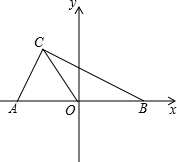 如图在平面直角坐标系中,A(a,0),B(b,0),(-1,2).且|2a+b+1|+
如图在平面直角坐标系中,A(a,0),B(b,0),(-1,2).且|2a+b+1|+| a+2b-4 |
(1)求a、b的值;
(2)①在y轴的正半轴上存在一点M,使S△COM=
| 1 |
| 2 |
②在坐标轴的其他位置是否存在点M,使S△COM=
| 1 |
| 2 |
考点:坐标与图形性质,三角形的面积
专题:计算题
分析:(1)根据非负数的性质得到
,然后解方程组即可得到a与b的值;
(2))①点A的坐标为(-2,0),点B的坐标为(3,0),若设M的坐标为(0,m),其中m>0,根据三角形面积公式得到
•1•m=
•
•2•5,解得m=5,则M点的坐标为(0,5);
②分类讨论:当M点在y轴上,设M的坐标为(0,m),根据三角形面积公式
•1•|m|=
•
•2•5;当M点在x轴上,设M的坐标为(n,0),根据三角形面积公式得
•2•|n|=
•
•2•5,然后分别解方程求出m和n的值即可得到满足条件的M点坐标.
|
(2))①点A的坐标为(-2,0),点B的坐标为(3,0),若设M的坐标为(0,m),其中m>0,根据三角形面积公式得到
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②分类讨论:当M点在y轴上,设M的坐标为(0,m),根据三角形面积公式
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)根据题意和非负数的性质得
,
解得
;
(2)①点A的坐标为(-2,0),点B的坐标为(3,0),
若设M的坐标为(0,m),
根据题意得
•1•m=
•
•2•5,
解得m=5,
所以M点的坐标为(0,5);
②存在.
当M点在y轴上,设M的坐标为(0,m),
根据题意得
•1•|m|=
•
•2•5,
解得m=±5,
此时M点的坐标为(0,5),(0,-5);
当M点在x轴上,设M的坐标为(n,0),
根据题意得
•2•|n|=
•
•2•5,
解得n=±2.5,
此时M点的坐标为(2.5,0),(2.5,0);
综上所述:M点的坐标为(0,5),(0,-5),(2.5,0),(-2.5,0).
|
解得
|
(2)①点A的坐标为(-2,0),点B的坐标为(3,0),
若设M的坐标为(0,m),
根据题意得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得m=5,
所以M点的坐标为(0,5);
②存在.
当M点在y轴上,设M的坐标为(0,m),
根据题意得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得m=±5,
此时M点的坐标为(0,5),(0,-5);
当M点在x轴上,设M的坐标为(n,0),
根据题意得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得n=±2.5,
此时M点的坐标为(2.5,0),(2.5,0);
综上所述:M点的坐标为(0,5),(0,-5),(2.5,0),(-2.5,0).
点评:本题考查了坐标与图形性质:利用点的坐标确定线段的长度和直线与坐标的位置关系.

练习册系列答案
相关题目
 如图,已知AB为⊙O的直径,PB与⊙O相切于点B,线段OP与弦BC垂直并相交于点D,OP与弧BC相交于点E,连接AC.
如图,已知AB为⊙O的直径,PB与⊙O相切于点B,线段OP与弦BC垂直并相交于点D,OP与弧BC相交于点E,连接AC. 如图,已知:△ABC中,AB=13,BD=5,AD=12,若DC=16,求AC的长.
如图,已知:△ABC中,AB=13,BD=5,AD=12,若DC=16,求AC的长.
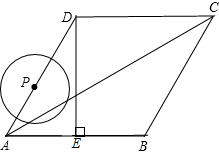 如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2,动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.
如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2,动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.