题目内容

7．已知一个等腰三角形的两条边长分别是$\sqrt{12}$和$\sqrt{18}$，求这个三角形的周长．

分析 根据题意可以分两种情况计算这个三角形的周长，从而可以解答本题．

解答 解：∵一个等腰三角形的两条边长分别是$\sqrt{12}$和$\sqrt{18}$，
∴这个三角形的周长是：$\sqrt{12}+\sqrt{12}+\sqrt{18}$=$4\sqrt{3}+3\sqrt{2}$或$\sqrt{12}+\sqrt{18}+\sqrt{18}=2\sqrt{3}+6\sqrt{2}$，
答：这个三角形的周长是$4\sqrt{3}+3\sqrt{2}$或$2\sqrt{3}+6\sqrt{2}$．

点评 本题考查二次根式的应用，解答本题的关键是明确题意，利用分类讨论的数学思想解答．

练习册系列答案
相关题目
17．若2x=3，2y=5，则2x+y=（　　）
A．11B．15C．30D．45
18．某校开展以“我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制的不完整的折线统计图和扇形统计图．
（1）在这次随机抽样调查中，共抽查了200名学生；
（2）把折线统计图补充完整；
（3）扇形统计图中，公务员部分对应的圆心角的度数72°；
（4）若从被调查的学生中任意抽取一名，求抽取的这名学生最喜欢的职业是“教师”的概率．
15．（1）如图（1），在Rt△ABC中，∠ACB=90°，∠B=60°，在图中作出∠ACB的三等分线CD，CE．（要求：尺规作图，保留作图痕迹，不写作法）
（2）由（1）知，我们可以用尺规作图作出直角的三等分线，但是仅仅使用尺规却不能把任意一个角分成三等分，为此，人们发明了许多等分角的机械器具，如图（2）是用三张硬纸片自制的一个最简单的三分角器，与半圆O相接的AB带的长度与半圆的半径相等；BD带的长度任意，它的一边与直线AC形成一个直角，且与半圆相切于点B，假设需要将∠KSM三等分，如图（3），首先将角的顶点S置于BD上，角的一边SK经过点A，另一边SM与半圆相切，连接SO，则SB，SO为∠KSM的三等分线，请你证明．
2．如图①，已知射线AB、CD，且AB∥CD．
（1）如图②，若E为平面内一点，探究∠A、∠C、∠AEC之间的数量关系，并证明你的结论．
（2）若E为平面内任意一点，请依据点E的不同位置分别画出示意图探究∠A、∠C、∠AEC之间的数量关系，并直接写出结论．（注：∠A、∠C、∠AEC均为锐角或钝角）
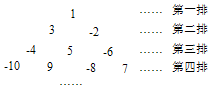12．将整数1，-2，3，-4，5，-6，…按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示实数9，则表示实数2017的有序实数对是（64，64）．
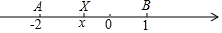19．我们知道一个数x的绝对值的几何意义是：在数轴上表示这个数x的点离原点（表示数0）的距离，x的绝对值表示为|x|，也可以写成|x-0|，比如|2|=|2-0|=2；
在数轴上表示两个数x，y的点之间的距离可以表示为|x-y|，比如，表示3的点与-1的点之间的距离表示为|3-（-1）|=|3+1|=4；
|x+2|+|x-1|可以表示点x与点1之间的距离跟点x与-2之间的距离的和，根据图示易知：当点X的位置在点A和点B之间（包含点A和点B）时，点X与点A的距离跟点X和点B的距离之和最小，且最小值为3，即|x+2|+|x-1|的最小值是3，且此时x的值为-2≤x≤1
请根据以上阅读，解答下列问题：
（1）|x+1|+|x-2|的最小值是3，此时x的值为-1≤x≤2；
（2）|x+2|+|x|+|x-1|的最小值是3，此时x的值为x=0；
（3）当|x+1|+|x|+|x-2|+|x-a|的最小值是4.5时，求出a的值及x的值．
16．计算下列各式的值（精确到0.001）
（1）$\sqrt{7}$-$\sqrt{6}$+$\sqrt{5}$
（2）$\root{3}{9}$+$\sqrt{2}$-π
（3）|$\sqrt{3}$-2|+2$\sqrt{3}$．
13．已知Rt△ABC中，∠A=90°，∠B=30°，CD平分∠ACB且与AB边交于点D，AC=$\sqrt{6}$，则点D到边BC的距离是（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．$\sqrt{6}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网