题目内容
6.图a是一个长为2m、宽为2n的长方形,沿图中实线用剪刀均分成四块小长方形然后按图b的形状拼成一个大正方形.(1)图b中的小正方形的边长等于m-n;
(2)图a中四个长方形的面积和为4mn;图b中四个小长方形的面积和还可以表示为(m+n)2-(m-n)2.
(3)由(2)写出代数式:(m+n)2,(m-n)2,mn之间的等量关系:(m+n)2-(m-n)2=4mn;
(4)根据(3)中的等量关系,解决如下问题:若x+y=8,xy=7,则(2x-2y)2=144.
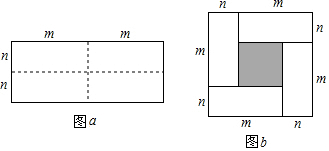
分析 (1)观察得到长为m,宽为n的长方形的长宽之差即为阴影部分的正方形的边长;
(2)根据长方形面积公式可求图a中四个长方形的面积和;可以用大正方形的面积减去先方形的面积得到图b中四个小长方形的面积和;
(3)利用(2)可以得到(m+n)2-(m-n)2=4mn;
(4)根据(3)的结论得到(2x-2y)2=4(x-y)2=4(x+y)2-16xy,然后把x+y=8,xy=7代入计算.
解答 解:(1)图b中的阴影部分的正方形的边长等于长为m,宽为n的长方形的长宽之差,即m-n;
(2)图a中四个长方形的面积和为4mn;图b中四个小长方形的面积和还可以表示为(m+n)2-(m-n)2;
(3)(m+n)2-(m-n)2=4mn;
(4)(2x-2y)2=4(x-y)2=4(x+y)2-16xy,
当x+y=8,xy=7时,原式=256-112=144.
故答案为:m-n;4mn;(m+n)2-4mn;(m+n)2-(m-n)2=4mn;144.
点评 本题考查了完全平方公式的几何背景:利用几何图形之间的面积关系得到完全平方公式.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
17.骑自相车旅行越来越受到人们的喜爱,顺风车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%.
(1)求今年4月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
(1)求今年4月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
11.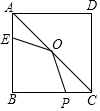 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )| A. | 4+3$\sqrt{2}$ | B. | $\sqrt{29}$+$\sqrt{5}$ | C. | 2+$\sqrt{5}$+3$\sqrt{2}$ | D. | $\sqrt{5}$+$\sqrt{2}$ |
15.阅读下面材料,解答后面问题:
小敏的作法如下:
判断小敏的作法是否正确?若正确,请证明;若不正确,请说明理由.
| 在数学课上,老师提出如下问题: 已知:Rt△ABC,∠ABC=90° 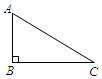 求作:矩形ABCD. |
①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=BO;③连接DA,DC.则四边形ABCD即为所求. |
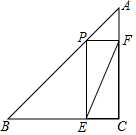 如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=4,点P是AB上的一个动点(点P与点A、B不重合),过点P分别作PE⊥BC于点E,PF⊥AC于点F,连接EF.
如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=4,点P是AB上的一个动点(点P与点A、B不重合),过点P分别作PE⊥BC于点E,PF⊥AC于点F,连接EF.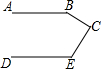 如图,AB∥DE,则∠B、∠C、∠E之间满足的数量关系是∠B+∠C+∠E=360°.
如图,AB∥DE,则∠B、∠C、∠E之间满足的数量关系是∠B+∠C+∠E=360°.