题目内容
15.阅读下面材料,解答后面问题:| 在数学课上,老师提出如下问题: 已知:Rt△ABC,∠ABC=90° 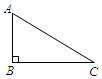 求作:矩形ABCD. |
①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=BO;③连接DA,DC.则四边形ABCD即为所求. |
分析 利用基本作图得到OA=OC,OB=OD,则利用平行四边形的判定方法可判断四边形ABCD为平行四边形,然后根据矩形的判定方法得到四边形ABCD为矩形.
解答 解:小敏的作法正确.理由如下:
∵线段AC的垂直平分线交AC于点O,
∴AO=CO,
∵BO=DO,
∴四边形ABCD为平行四边形,
∵∠ABC=90°,
∴四边形ABCD为矩形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了矩形的判定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.正方形具有而菱形不一定具有的性质是( )
| A. | 对角线平分一组对角 | B. | 对角线互相垂直平分 | ||
| C. | 对角线相等 | D. | 四条边相等 |
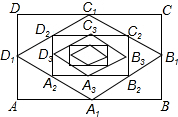 如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3;…这样继续下去.则图中的四边形A8B8C8D8的周长等于4,图中的四边形AnBnCnDn的面积等于192×($\frac{1}{2}$)n.
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3;…这样继续下去.则图中的四边形A8B8C8D8的周长等于4,图中的四边形AnBnCnDn的面积等于192×($\frac{1}{2}$)n. 已知一次函数y=2x-4.
已知一次函数y=2x-4.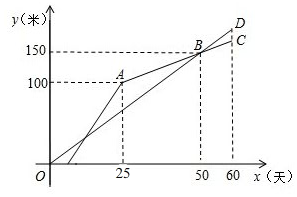 甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.
甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.